二叉树的深度优先
# 二叉树的深度优先
# lc124. 二叉树的最大路径困难hot
题目描述
路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ，返回其 最大路径和 。
示例 1：
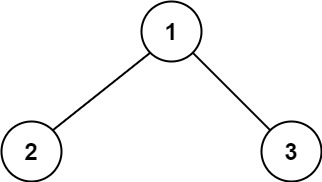
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6
1
2
3
2
3
示例 2：
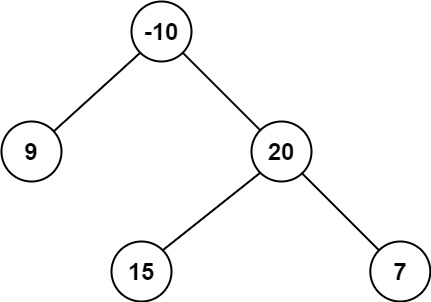
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42
1
2
3
2
3
思路
使用递归，因为树每次只能进入一侧，所以每一轮贡献的值只能是当前根节点+左边节点或根节点+右节点和0之间的最大值,记为max并返回
因为有可能是root -> root.left -> root.right组成的值比 root.root -> root -> root.left/right还要大，记为sum，然后更新到全局变量中
/**
* @param {TreeNode} root
* @return {number}
*/
var maxPathSum = function(root) {
// 设置一个全局最小的和
let sum = Number.MIN_SAFE_INTEGER
const dfs = node => {
if(!node) return 0
const left = dfs(node.left)
const right = dfs(node.right)
// 算出路径最大的和，替换全局的sum
sum = Math.max(sum, left + node.val + right)
// 返回每一轮最大的值
const max = Math.max(left, right) + node.val
return max > 0 ? max : 0
}
dfs(root)
return sum
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
- 时间复杂度：
O(N)，其中N是二叉树中的节点个数。对每个节点访问不超过2次。 - 空间复杂度：
O(N)，其中N是二叉树中的节点个数。空间复杂度主要取决于递归调用层数，最大层数等于二叉树的高度，最坏情况下，二叉树的高度等于二叉树中的节点个数。
# lc543. 二叉树的直径简单hot
题目描述
给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/ \
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]
1
2
3
4
5
6
7
8
2
3
4
5
6
7
8
- 直径定义为任意两个节点间路径的最长长度（这里长度指边的数量）。
- 这条路径可以经过根节点，也可以不经过根节点。
- 对每个节点，最长路径可能是：
- 左子树的最大直径（不经过当前节点）
- 右子树的最大直径（不经过当前节点）
- 当前节点的左右子树最大深度之和（路径经过当前节点）
解题思路
- 对节点递归计算其左右子树的深度（深度是节点到叶子节点最长路径的边数）。
- 对每个节点，用
leftDepth + rightDepth更新全局最大直径。 - 返回当前节点的最大深度
max(leftDepth, rightDepth) + 1给父节点。
var diameterOfBinaryTree = function(root) {
let res = 0
const depth = node => {
if(!node) return 0
const left = depth(node.left)
const right = depth(node.right)
// 计算最大直径 更新到全局res上
res = Math.max(res, left + right)
// 每轮返回左子树和右子树中的最大值
return Math.max(left, right) + 1
}
depth(root)
return res
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2
3
4
5
6
7
8
9
10
11
12
13
14
时间复杂度O(n)
空间复杂度O(h) h为二叉树的最大深度，是一个常数变量
# lc257. 二叉树的所有路径简单
题目描述
给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1：
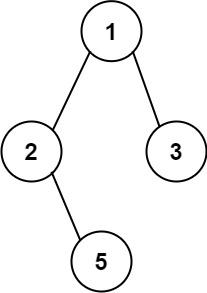
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]
1
2
2
示例 2：
输入：root = [1]
输出：["1"]
1
2
2
var binaryTreePaths = function(root) {
if(!root) return []
const res = []
const binary = (node, str) => {
if(!node.left && !node.right) {
str += node.val
res.push(str)
return
}
str += `${node.val}->`
if(node.left) binary(node.left, str)
if(node.right) binary(node.right, str)
}
binary(root, '')
return res
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
- 时间复杂度：
O(N)，其中N表示节点数目。在深度优先搜索中每个节点会被访问一次且只会被访问一次，每一次会对path变量进行拷贝构造，时间代价为O(N)，故时间复杂度为O(N)； - 空间复杂度：
O(N)，其中N表示节点数目。除答案数组外我们需要考虑递归调用的栈空间。在最坏情况下，当二叉树中每个节点只有一个孩子节点时，即整棵二叉树呈一个链状，此时递归的层数为N，此时每一层的path变量的空间代价的总和的空间复杂度为O(N)，最好情况下，当二叉树为平衡二叉树时，它的高度为logN，此时空间复杂度为O((logN)2)。
# lc98. 验证二叉搜索树中等hot
题目描述
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下：
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1：
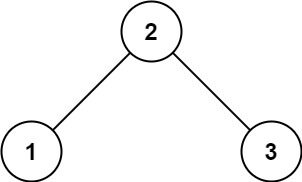
输入：root = [2,1,3]
输出：true
1
2
3
2
3
示例 2：
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。
1
2
3
4
5
2
3
4
5
递归过程中，给每个节点维护一个 值的范围 [min, max]。
节点值必须满足 min < 节点值 < max。
根节点初始范围是 (-∞, +∞)。
递归检查左子树，范围变成 [min, node.val)。
递归检查右子树，范围变成 (node.val, max]。
var isValidBST = function(root) {
const dfs = (root, minVal, maxVal) => {
if(!root) return true
if(root.val <= minVal || root.val >= maxVal) return false
return dfs(root.left, minVal, root.val) && dfs(root.right, root.val, maxVal)
}
return dfs(root, -Infinity, +Infinity)
};
1
2
3
4
5
6
7
8
9
10
11
2
3
4
5
6
7
8
9
10
11
- 时间复杂度 :
O(n)，其中n为二叉树的节点个数。二叉树的每个节点最多被访问一次，因此时间复杂度为O(n)。 - 空间复杂度 :
O(n)，其中n为二叉树的节点个数。栈最多存储n个节点，因此需要额外的O(n)的空间。
# lc98. 递归遍历文件
// 输入格式;
const nodes = {
name: 'page.js',
require: [
{
name: 'A.js',
require: [
{
name: 'C.js',
require: [
{ name: 'F.js', require: [] }
]
},
{
name: 'B.js',
require: [
{
name: 'D.js',
require: [
{ name: 'F.js', require: [] }
]
},
{ name: 'E.js', require: [] }
]
}
]
}
]
};
Const genRequireTree=(node)+>{
//写代码
Console.log(genRequire Tree(node))
要求输出:["F.js", "E.js", "D.js", "C.js", "B.js", "A.js", "page.js"]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
const genRequireTree = (node) => {
const result = [];
const dfs = (n) => {
if (!n) return;
if (Array.isArray(n.require)) {
for (const dep of n.require) {
dfs(dep);
}
}
result.push(n.name);
};
dfs(node);
return result;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
上次更新: 2025/06/08, 23:39:58