二叉树的广度优先

# 二叉树的广度优先

# lc637. 二叉树的层平均值简单

题目描述

给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。

提示：

节点值的范围在32位有符号整数范围内。

示例 1：

输入：
    3
   / \
  9  20
    /  \
   15   7

输出：[3, 14.5, 11]

解释：
第 0 层的平均值是 3 ,  第1层是 14.5 , 第2层是 11 。因此返回 [3, 14.5, 11]

1
2
3
4
5
6
7
8
9
10
11

思路就是层序遍历多一步

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var averageOfLevels = function(root) {
  const res =  []
  const queue = [root]
  while(queue.length) {
    let sum = 0
    let queuelen = queue.length
    let len = queuelen
    while(queuelen--) {
      let node = queue.shift()
      sum += node.val
      if(node.left) queue.push(node.left)
      if(node.right) queue.push(node.right)
    }
    res.push(sum / len)    
  }
  return res
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

时间复杂度O(n)

空间复杂度O(n)

# lc199. 二叉树的右视图中等hot

题目描述

给定一个二叉树的根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

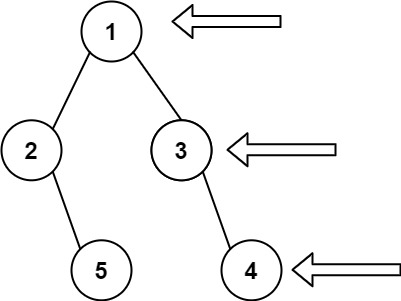
输入: [1,2,3,null,5,null,4]

输出: [1,3,4]

1
2
3

示例 2:

输入: [1,null,3]

输出: [1,3]

1
2
3

示例 3:

输入: []

输出: []

1
2
3

思路

层序遍历

// BFS
function rightSideView(root) {
  if (!root) return [];

  const queue = [root];
  const result = [];

  while (queue.length > 0) {
    const size = queue.length;
    let rightNode = null;

    for (let i = 0; i < size; i++) {
      const node = queue.shift();

      // 记录当前层最后一个节点
      rightNode = node;

      if (node.left) queue.push(node.left);
      if (node.right) queue.push(node.right);
    }

    result.push(rightNode.val);
  }

  return result;
}

// DFS
function rightSideView(root) {
  const result = [];

  function dfs(node, depth) {
    if (!node) return;

    // 第一次访问该深度时，加入节点值（优先右子树）
    if (depth === result.length) {
      result.push(node.val);
    }

    dfs(node.right, depth + 1);
    dfs(node.left, depth + 1);
  }

  dfs(root, 0);
  return result;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# lc222. 完全二叉树的节点个数中等

题目描述

给你一棵完全二叉树的根节点 root ，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

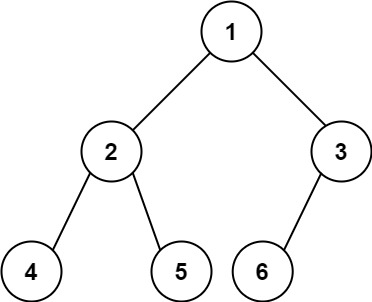
输入：root = [1,2,3,4,5,6]

输出：6

1
2
3

示例 2：

输入：root = []

输出：0

1
2
3

示例 3：

输入：root = [1]

输出：1

1
2
3

// BFS
var countNodes = function(root) {
  if(!root) return 0
  const queue = [root]
  let res = 0
  while(queue.length) {
    let node = queue.shift()
    if(node) res++
    if(node.left) queue.push(node.left)
    if(node.right) queue.push(node.right)
  }
  return res
};

// DFS
var countNodes = function(root) {
    if(!root) return 0
    return 1 + countNodes(root.left) + countNodes(root.right)
}
// 二分法
var countNodes = function(root) {
    if(!root) return 0

    let leftHeight = 0, rightHeight = 0
    let leftNode = root, rightNode = root

    while(leftNode){
        leftHeight++
        leftNode = leftNode.left
    }
    while(rightNode){
        rightHeight++
        rightNode = rightNode.right
    }
    if(leftHeight === rightHeight) return 2 ** leftHeight - 1

    return 1 + countNodes(root.left) + countNodes(root.right)
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# lc404. 左叶子之和简单

题目描述

计算给定二叉树的所有左叶子之和。

示例：

    3
   / \
  9  20
    /  \
   15   7

在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

1
2
3
4
5
6
7

思路:层序遍历

初始化一个queue来保存当前层的元素，遍历队列中的元素，如果该节点的左子树不存在左右子树，说明它是一个左叶子节点，将其加在结果上。

var sumOfLeftLeaves = function(root) {
  if(!root) return 0
  const queue = [root]
  let res = 0
  while(queue.length) {
    let node = queue.shift()
    if(node.left) {
     if(!node.left.left && !node.left.right) {
       res += node.left.val
     } 
     queue.push(node.left)
    }
    if(node.right) queue.push(node.right)
  }
  return res
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

时间复杂度O(n)

空间复杂度O(n)

# lc513. 找树左下角的值中等

题目描述

给定一个二叉树的根节点 root，请找出该二叉树的最底层最左边节点的值。

假设二叉树中至少有一个节点。

示例 1:

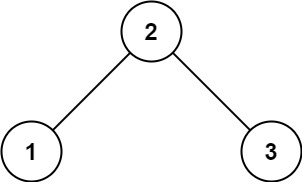
输入: root = [2,1,3]

输出: 1

1
2
3

示例 2:

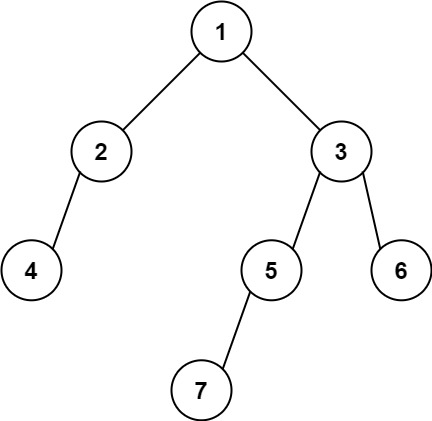
输入: [1,2,3,4,null,5,6,null,null,7]

输出: 7

1
2
3

思路

对二叉树进行层序遍历，然后从右开始入队，然后左子节点入队
对队列元素依次出队，数组最后一个值就是二叉树左下角的值

var findBottomLeftValue = function(root) {
  const res = []
  const queue = [root]
  while(queue.length) {
    let node = queue.shift()
    res.push(node.val)
    node.right && queue.push(node.right)
    node.left && queue.push(node.left)
  }
  return res[res.length - 1]
};

1
2
3
4
5
6
7
8
9
10
11

时间复杂度：O(n)，其中n是二叉树的节点数，我们需要遍历整棵树；
空间复杂度：O(n)，其中n是二叉树的高度，我们需要初始化一个数组来保存二叉树的所有节点；

# lc662. 二叉树最大宽度中等hot

题目描述

给定一个二叉树，编写一个函数来获取这个树的最大宽度。树的宽度是所有层中的最大宽度。这个二叉树与满二叉树（full binary tree）结构相同，但一些节点为空。

每一层的宽度被定义为两个端点（该层最左和最右的非空节点，两端点间的null节点也计入长度）之间的长度。

示例 1:

输入: 
           1
         /   \
        3     2
       / \     \  
      5   3     9
      
输出: 4

解释: 最大值出现在树的第 3 层，宽度为 4 (5,3,null,9)

1
2
3
4
5
6
7
8
9
10

示例 2:

输入: 
          1
         /  
        3    
       / \       
      5   3     
      
输出: 2

解释: 最大值出现在树的第 3 层，宽度为 2 (5,3)

1
2
3
4
5
6
7
8
9
10

示例 3:

输入: 
          1
         / \
        3   2 
       /        
      5      

输出: 2

解释: 最大值出现在树的第 2 层，宽度为 2 (3,2)

1
2
3
4
5
6
7
8
9
10

示例 4:

输入: 
          1
         / \
        3   2
       /     \  
      5       9 
     /         \
    6           7

输出: 8

解释: 最大值出现在树的第 4 层，宽度为 8 (6,null,null,null,null,null,null,7)

1
2
3
4
5
6
7
8
9
10
11
12

注意: 答案在32位有符号整数的表示范围内。

var widthOfBinaryTree = function(root) {
    if (!root) return 0;

    let maxWidth = 0;
    let queue = [[root, 0]]; // [node, position]

    while (queue.length > 0) {
        let size = queue.length;
        let levelMin = queue[0][1]; // 当前层最左边的编号（用于位置归一）

        let first = 0, last = 0;

        for (let i = 0; i < size; i++) {
            let [node, pos] = queue.shift();
            pos -= levelMin; // 归一化，防止整数溢出
            if (i === 0) first = pos;
            if (i === size - 1) last = pos;

            if (node.left) {
                queue.push([node.left, 2 * pos]);
            }
            if (node.right) {
                queue.push([node.right, 2 * pos + 1]);
            }
        }

        maxWidth = Math.max(maxWidth, last - first + 1);
    }

    return maxWidth;
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

时间复杂度：O(n)，其中n是二叉树的节点数，我们需要遍历完整个二叉树；
空间复杂度：O(n)，其中n是nodes栈的长度。

# lc111. 二叉树的最小深度简单

题目描述

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

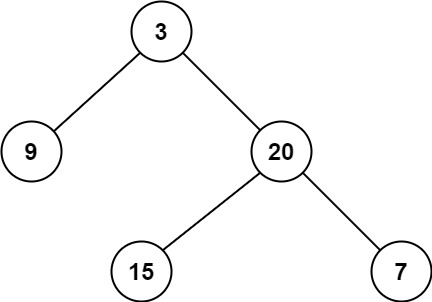
输入：root = [3,9,20,null,null,15,7]

输出：2

1
2
3

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]

输出：5

1
2
3

思路:层序遍历

左右子节点入队，假设他没有左右节点那就马上终止程序，然后当前的深度

var minDepth = function(root) {
  if(!root) return 0
  const queue = [root]
  let level = 1
  while(queue.length) {
    let queuelen = queue.length
    while(queuelen--) {
      let node = queue.shift()
      if(!node.left && !node.right) return level
      node.left && queue.push(node.left)
      node.right && queue.push(node.right)
    }
    level++
  }
  return level
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

时间复杂度：O(n)，其中 n 是树的节点数。对每个节点访问一次。
空间复杂度：O(n)，其中 n 是树的节点数。空间复杂度主要取决于队列的开销，队列中的元素个数不会超过树的节点数。

dfs

var minDepth = function(root) {
  if(!root) return 0
  if(!root.left && !root.right) return 1
  if(!root.left || !root.right) return root.left ? minDepth(root.left) + 1 : minDepth(root.right) + 1
  return 1 + Math.min(minDepth(root.left), minDepth(root.right))
};

1
2
3
4
5
6

时间复杂度：O(N)，其中 N是树的节点数。对每个节点访问一次。

空间复杂度：O(H)，其中 H 是树的高度。空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 O(logN)。

# lc297. 二叉树的序列化与反序列化困难hot

题目描述

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

提示: 输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

示例 1：

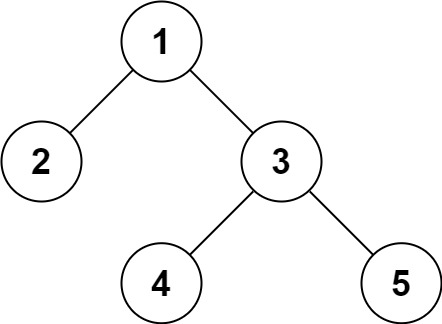
输入：root = [1,2,3,null,null,4,5]

输出：[1,2,3,null,null,4,5]

1
2
3

示例 2：

输入：root = []

输出：[]

1
2
3

示例 3：

输入：root = [1]

输出：[1]

1
2
3

示例 4：

输入：root = [1,2]

输出：[1,2]

1
2
3

BFS

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */

/**
 * Encodes a tree to a single string.
 *
 * @param {TreeNode} root
 * @return {string}
 */
var serialize = function(root) {
    if(!root) return []
    const res = []
    const queue = [root]
    while(queue.length) {
      let queuelen = queue.length
      while(queuelen--) {
        let node = queue.shift()
        res.push(node ? node.val : null)
        if(node) {
          queue.push(node.left)
          queue.push(node.right)
        }
      }
    }
  return res
};

/**
 * Decodes your encoded data to tree.
 *
 * @param {string} data
 * @return {TreeNode}
 */
var deserialize = function(data) {
    const len = data.length
    if(!len) return null
    const root = new TreeNode(data.shift())
    const queue = [root]
    while(queue.length){
        // 取出将要遍历的节点
        const node = queue.shift()
        if(!data.length){
            break
        }
        // 还原左节点
        const leftVal = data.shift()
        if(leftVal === null){
            node.left = null
        }else{
            node.left = new TreeNode(leftVal)
            queue.push(node.left)
        }
        if(!data.length){
            break
        }

        // 还原右节点
        const rightVal = data.shift()
        if(rightVal === null){
            node.right = null
        }else{
            node.right = new TreeNode(rightVal)
            queue.push(node.right)
        }
    }
    return root
};

/**
 * Your functions will be called as such:
 * deserialize(serialize(root));
 */

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

时间复杂度：在序列化和反序列化函数中，我们只访问每个节点一次，因此时间复杂度为 O(n)，其中 n 是节点数，即树的大小。
空间复杂度：在序列化和反序列化函数中，我们递归会使用栈空间，故渐进空间复杂度为 O(n)。

DFS

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */

/**
 * Encodes a tree to a single string.
 *
 * @param {TreeNode} root
 * @return {string}
 */
var serialize = function(root) {
    const result = []
    function traverseNode(node){
        if(node === null){
            result.push(null)
        }else{
            result.push(node.val)
            traverseNode(node.left)
            traverseNode(node.right)
        }
    }
    traverseNode(root)
    return result
};

/**
 * Decodes your encoded data to tree.
 *
 * @param {string} data
 * @return {TreeNode}
 */
var deserialize = function(data) {
    const len = data.length
    if(!len){
        return null
    }
    let i = 0
    function structure (){
        // 递归停止条件
        if(i >= len){
            return null
        }
        const val = data[i]
        i++
        if(val === null){
            return null
        }
        const node = new TreeNode(val)
        node.left = structure()
        node.right = structure()
        return node
    }
    return structure()
};

/**
 * Your functions will be called as such:
 * deserialize(serialize(root));
 */

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

时间复杂度：在序列化和反序列化函数中，我们只访问每个节点一次，因此时间复杂度为 O(n)，其中 n 是节点数，即树的大小。
空间复杂度：在序列化和反序列化函数中，我们递归会使用栈空间，故渐进空间复杂度为 O(n)。

上次更新: 2025/06/04, 10:21:03

← 二叉树的遍历二叉树的深度优先→