回溯

lc46. 全排列中等hot

题目描述

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

思路

由题可得如果用暴力法面试会被直接挂掉，或者算法超时，可以采用dfs + 回溯(撤销)进行解答

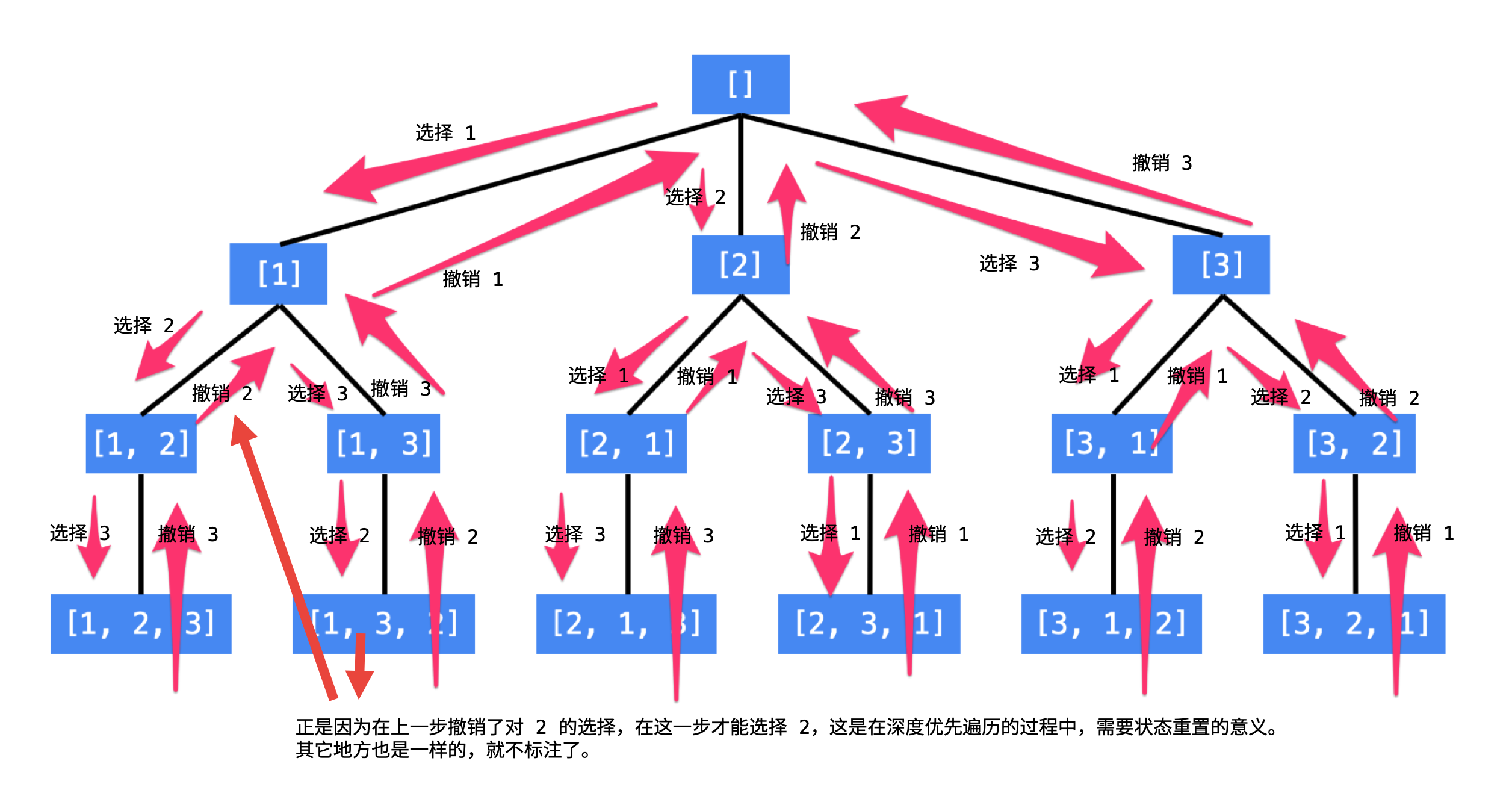
看了这个图就对这道全排列比较直观了，同时也有一定的解题模版

const result = []
function backtrack(路径, 选择列表) {
    if 满足结束条件:
        result.push(路径)
        return
    
    for 选择 of 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择
}

下面就来干起

function permute(nums: number[]): number[][] {
  const res: number[][] = [];
  const path: number[] = [];
  const used = new Array(nums.length).fill(false);

  function backtrack() {
    if (path.length === nums.length) {
      res.push([...path]); // 注意要复制
      return;
    }

    for (let i = 0; i < nums.length; i++) {
      if (used[i]) continue;

      path.push(nums[i]);
      used[i] = true;

      backtrack(); // 递归进入下一层

      // 回溯
      path.pop();
      used[i] = false;
    }
  }

  backtrack();
  return res;
}

时间复杂度:O(n×n!)

O(n * n!)

为什么是 n!：

• 第一层 有 n 个选择
• 第二层 有 n - 1 个选择
• ...
• 第 n 层 有 1 个选择

每次找到一个合法排列时，我们会 res.push([...path])，这一步是 O(n) 的（因为要复制 path）

空间复杂度：O(n)

递归栈最大深度为 n

used 数组长度是 n

path 临时列表最大长度也是 n

lc47. 全排列 II中等hot

题目描述

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

思路：和全排列一 一样但是多了去重

function permuteUnique(nums: number[]): number[][] {
  const res: number[][] = [];
  const path: number[] = [];
  const used: boolean[] = new Array(nums.length).fill(false);

  nums.sort();

  function backtrack() {
    if (path.length === nums.length) {
      res.push([...path]);
      return;
    }

    for (let i = 0; i < nums.length; i++) {
      // 去重关键条件：前一个相同数字用过才行
      if (used[i]) continue;
      // nums[i] === nums[i - 1] 比较好理解
      // !used[i - 1]的原因是如果是[1, 1, 2],当他回溯到最上层，path为[],轮到第二个1开始的时候，他会判断 used[i - 1]是false，表示当前同一级的还没用过，但是他前一个数又是一样的，那包重复了
      if (i > 0 && nums[i] === nums[i - 1] && !used[i - 1]) continue;

      path.push(nums[i]);
      used[i] = true;
      backtrack();
      path.pop();
      used[i] = false;
    }
  }

  backtrack();
  return res;
}

时间复杂度:O(n×n!)

空间复杂度：O(n)

剑指 Offer 38. 字符串的排列

题目描述

输入一个字符串，打印出该字符串中字符的所有排列。

你可以以任意顺序返回这个字符串数组，但里面不能有重复元素。

示例一:

输入：s = "abc"
输出：["abc","acb","bac","bca","cab","cba"]

示例二

输入：s = "aab"
输出：["aab","aba","baa"]

思路

和全排列II 不一样的地方在于本题可以用set来去重字符串

跟前面的有一点区别是他的字母是有可能重复的

var permutation = function(s) {
  const res = new Set(), visited = {}
  const dfs = (track) => {
    if(track.length === s.length) {
      // res.push(track)
      res.add(track)
      return
    }

    for(let i = 0; i < s.length; i++) {
      if(visited[i]) continue
      
      visited[i] = true
      dfs(track + s[i])
      visited[i] = false 
    }
  }
  dfs('')
  return [...res]
};

lc77. 组合中等hot

题目描述

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

思路

还是套模版,只不过原来的按模版的会超时，我们可以剪一下枝

var combine = function(n, k) {
  const res = []
  let start = 1
  const dfs = (start, nums) => {
    if(nums.length === k) {
      res.push([...nums])
      return
    }
    for(let i = start; i <= n; i++) {
      if(nums.includes(i)) {
        continue
      } else {
        nums.push(i)
        dfs(i + 1, nums)
        nums.pop()
      }
    }
  }
  dfs(start, [])
  return res
};

时间复杂度:O(C(n, k) * n),参照上面的全排列，C(n, k) = n! / (n - k)!

空间复杂度:O(n)递归的深度是n

lc93. 复原 IP 地址中等hot

题目描述

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

• 例如："0.1.2.201" 和"192.168.1.1" 是 有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "[email protected]" 是 无效 IP 地址。

给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

示例 1：

输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

示例 2：

输入：s = "0000"
输出：["0.0.0.0"]

示例 3：

输入：s = "101023"
输出：["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]

var restoreIpAddresses = function(s) {
  const len = s.length
  const res = []

  const findIP = (start, path) => {

    if(path.length === 4 && start >= len) {
      res.push(path.join('.'))
      return 
    }

    for(let i = start; i < len; i++) {
      const str = s.slice(start, i + 1)
      if(isValid(str)) {
        path.push(str)
        findIP(i + 1, path)
        path.pop()
      } else break
    }
  }

  const isValid = (str) => {
    if(str.length > 4) return false
    if(parseInt(str, 10) > 255) return false
    if(str.length > 1 && str[0] === '0') return false

    return true
  }

  findIP(0, [])

  return res
};

时间复杂度：O(3⁴) = O(81) 常数级别，最多枚举每段长度为 1~3 的组合。

空间复杂度：O(n) 递归栈 + O(m) 结果集（m 为返回的结果数）

lc78. 子集中等

题目描述

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

思路

这一道题就可以套模板了，只不过这里的dfs的push要在if外面，因为输出的res不一定与nums的length相等

var subsets = function(nums) {
  const result = [];
  helper(nums, 0, [], result);
  return result;
};

function helper(nums, start, track, result) {

  result.push([...track]);

  if (track.length === nums.length) {
    return
  }

  for (let i = start; i < nums.length; i++) {
    track.push(nums[i]);
    helper(nums, i + 1, track, result);
    track.pop();
  }
}

时间复杂度：O(2^n)，每个元素都有选/不选两种情况

空间复杂度：O(n)，递归栈最大深度为 n

lc139. 单词拆分中等

题目描述

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。

注意： 不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

示例 1：

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。

示例 2：

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
     注意，你可以重复使用字典中的单词。

示例 3：

输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

动态规划

• 设 dp[i] 表示字符串 s 的前 i 个字符（即 s[0...i-1]）是否可以被字典单词拼接出来。
• 初始化：dp[0] = true 表示空字符串可以被拆分。
• 状态转移：
  • 对每个 i（1 到 s.length）
  • 遍历 j 从 0 到 i-1
  • 如果 dp[j] 是 true，且 s[j...i-1] 在字典中出现，则令 dp[i] = true
• 最终答案为 dp[s.length]

var wordBreak = function(s, wordDict) {
  const wordSet = new Set(wordDict);
  const n = s.length;
  const dp = new Array(n + 1).fill(false);
  dp[0] = true;

  for (let i = 1; i <= n; i++) {
    for (let j = 0; j < i; j++) {
      if (dp[j] && wordSet.has(s.substring(j, i))) {
        dp[i] = true;
        break;  // 找到一个符合的即可跳出内层循环
      }
    }
  }

  return dp[n];
};

• 外层循环 i 从 1 到 n，共 n 次。
• 内层循环 j 最坏情况也遍历到 i-1，平均也接近 n。
• s.substring(j, i) 是截取字符串，时间复杂度是 O(i-j)，最坏情况是 O(n)。
• wordSet.has() 是哈希查找，平均 O(1)。

综合来看，最坏情况下每次判断 s.substring(j, i) 是 O(n)，加上两层循环，时间复杂度大致是：O(n^3)

空间复杂度

• dp 数组大小是 n+1，即 O(n)。
• wordSet 存储字典，空间为字典中所有单词长度总和，记为 m。
• 临时截取的子串空间，视语言实现而定，通常可以忽略。

思路

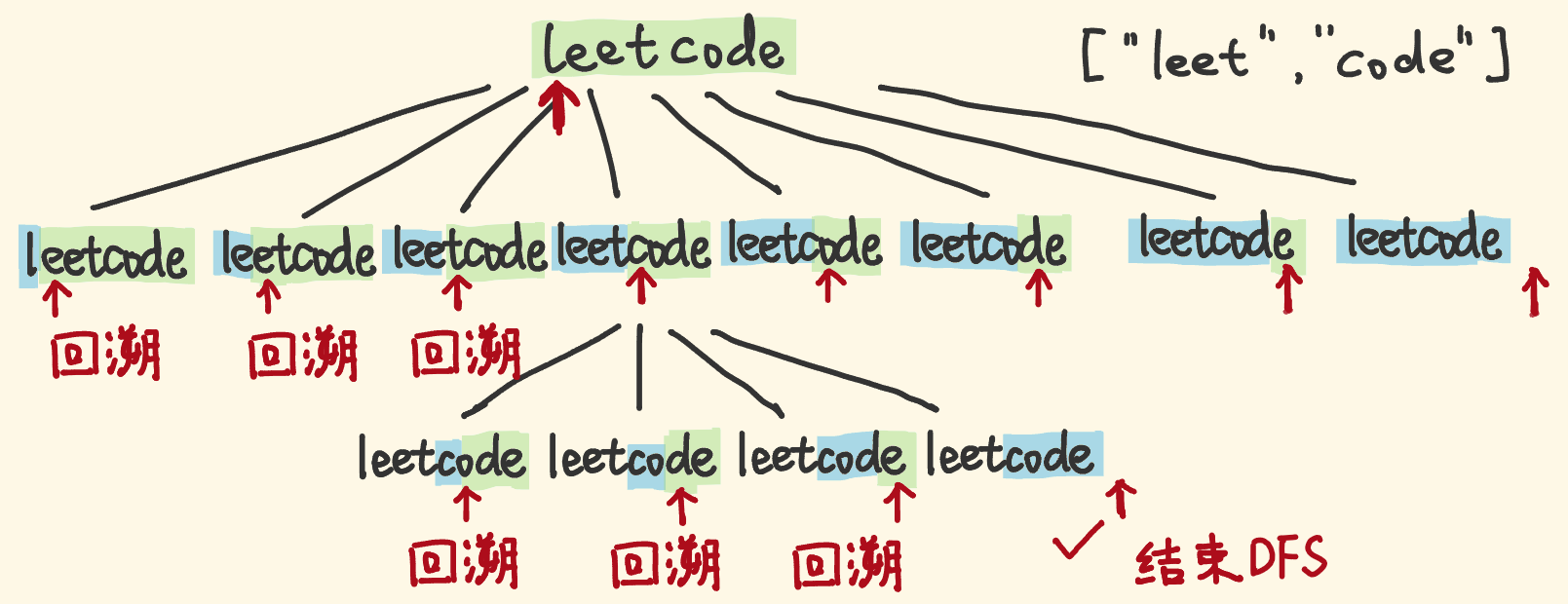
function wordBreak(s, wordDict) {
  const wordSet = new Set(wordDict);

  function backtrack(start) {
    if (start === s.length) return true;

    for (let end = start + 1; end <= s.length; end++) {
      const word = s.substring(start, end);
      if (wordSet.has(word) && backtrack(end)) {
        return true;
      }
    }
    return false;
  }

  return backtrack(0);
}

复杂度分析

时间复杂度

• 最坏情况下，backtrack 会在每个位置尝试切割所有可能的子串。
• 对于字符串长度为 n，每次递归最多尝试 O(n) 种切割。
• 递归深度最多为 n。

因此，时间复杂度近似为： O(n^n)

极端情况下，爆炸性组合导致指数级时间复杂度。

---

空间复杂度

• 递归调用栈最大深度为 n，即 O(n)。
• 额外使用了一个 Set 来存储字典，空间复杂度为字典大小，通常忽略。

所以空间复杂度主要是：O(n)

记忆化回溯

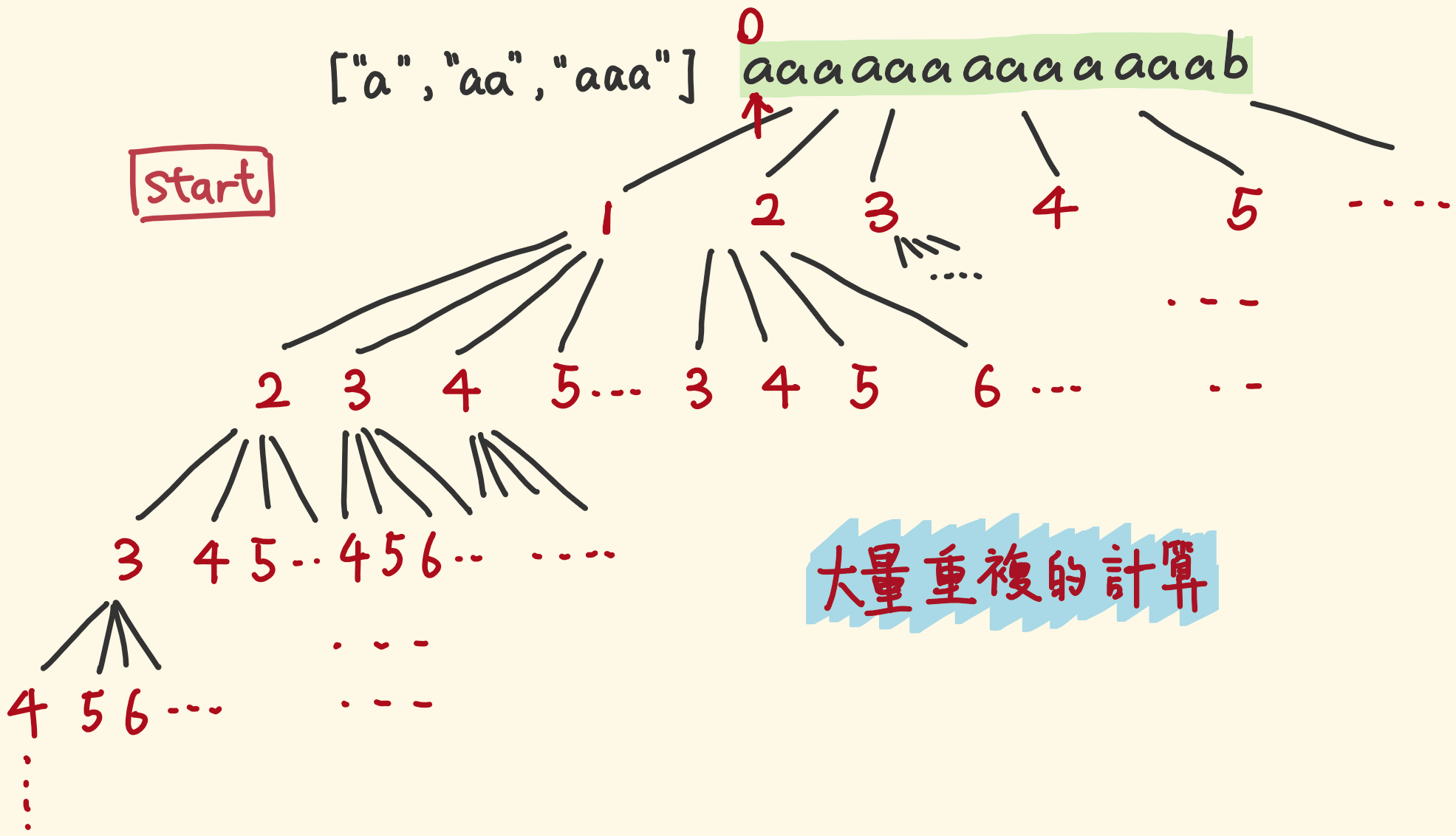
const wordBreak = (s, wordDict) => {
	const len = s.length;
  const wordSet = new Set(wordDict);
  const memo = new Array(len)
	const canBreak = (start) => { // 判断从start到末尾的子串能否break
		if (start == len) {//指针越界，s一步步成功划分为单词，才走到越界这步，现在没有剩余子串
			return true;   //返回真，结束递归
		}
    if(memo[start] !== undefined) return memo[start] // memo中有，就用memo中的
		for (let i = start + 1; i <= len; i++) { //指针i去划分两部分，for枚举出当前所有的选项i
			const prefix = s.slice(start, i);    // 切出的前缀部分
			if (wordSet.has(prefix) && canBreak(i)) {// 前缀部分是单词，且剩余子串能break，返回真
      memo[start] = true
				return true;                            
			} // 如果前缀部分不是单词，就不会执行canBreak(i)。进入下一轮迭代，再切出一个前缀串，再试
		}
    memo[start] = false
		return false; // 指针i怎么划分，都没有返回true，则返回false
	}

	return canBreak(0); // 递归的入口，从0到末尾的子串能否break
}

时间复杂度分析

假设：

• n = 字符串 s 的长度
• m = 字典中单词的最大长度（一般认为常数或小于 n）

. 递归次数（状态数）

• memo 数组长度是 n，每个索引 start 只会被计算一次（因为计算完后结果缓存起来了）。
• 因此，递归状态数最多为 O(n)。

---

2. 每次递归中的工作

• 在 start 位置，我们尝试从 start 到 start + len 的每个子串是否在字典中。
• 假设最长单词长度为 m，每次尝试的子串数最多为 m。
• 对每个子串，需要做一次字典查找（哈希查找平均 O(1)），再递归调用。

总体时间复杂度

• 最多调用 O(n) 个状态，
• 每个状态最多检查 m 个子串，

因此整体时间复杂度是：O(n * m)

空间复杂度

1. 递归栈空间

• 最坏情况下，递归深度最多为字符串长度 n，因为每次递归至少推进一个字符（start 递增）。
• 因此，递归调用栈空间为 O(n)。

1. memo 数组空间

• memo 通常是一个长度为 n 的数组，用于缓存每个起点的结果（true/false 或其它状态）。
• 所以 memo 占用空间为 O(n)。

1. 字典存储空间

• 假设字典以哈希表形式存储，大小为 d（字典中单词个数及长度综合），通常忽略在字符串 s 相关复杂度中。

---

综合空间复杂度

• 递归栈空间 + memo 空间
• 即 O(n) + O(n) = O(n)

lc140. 单词拆分 II困难

题目描述

给定一个字符串 s 和一个字符串字典 wordDict ，在字符串 s 中增加空格来构建一个句子，使得句子中所有的单词都在词典中。以任意顺序 返回所有这些可能的句子。

注意： 词典中的同一个单词可能在分段中被重复使用多次。

示例 1：

输入:s = "catsanddog", wordDict = ["cat","cats","and","sand","dog"]
输出:["cats and dog","cat sand dog"]

示例 2：

输入:s = "pineapplepenapple", wordDict = ["apple","pen","applepen","pine","pineapple"]
输出:["pine apple pen apple","pineapple pen apple","pine applepen apple"]
解释: 注意你可以重复使用字典中的单词。

示例 3：

输入:s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
输出:[]

思路

var wordBreak = function (s, wordDict) {
  let arr = [];
  function backTree(n, path) {
    if (n === s.length) {
      arr.push(path);
    } else {
      for (let i = 1; i <= s.length - n; i++) {
        if (wordDict.indexOf(s.substr(n, i)) !== -1) {
          if (n !== 0) {
            backTree(n + i, path + " " + s.substr(n, i));
          } else {
            backTree(n + i, path + s.substr(n, i));
          }
        }
      }
    }
  }
  backTree(0, "");
  return arr;
};

lc22. 括号生成中等hot

题目描述

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

思路

可以看成🌲的dfs

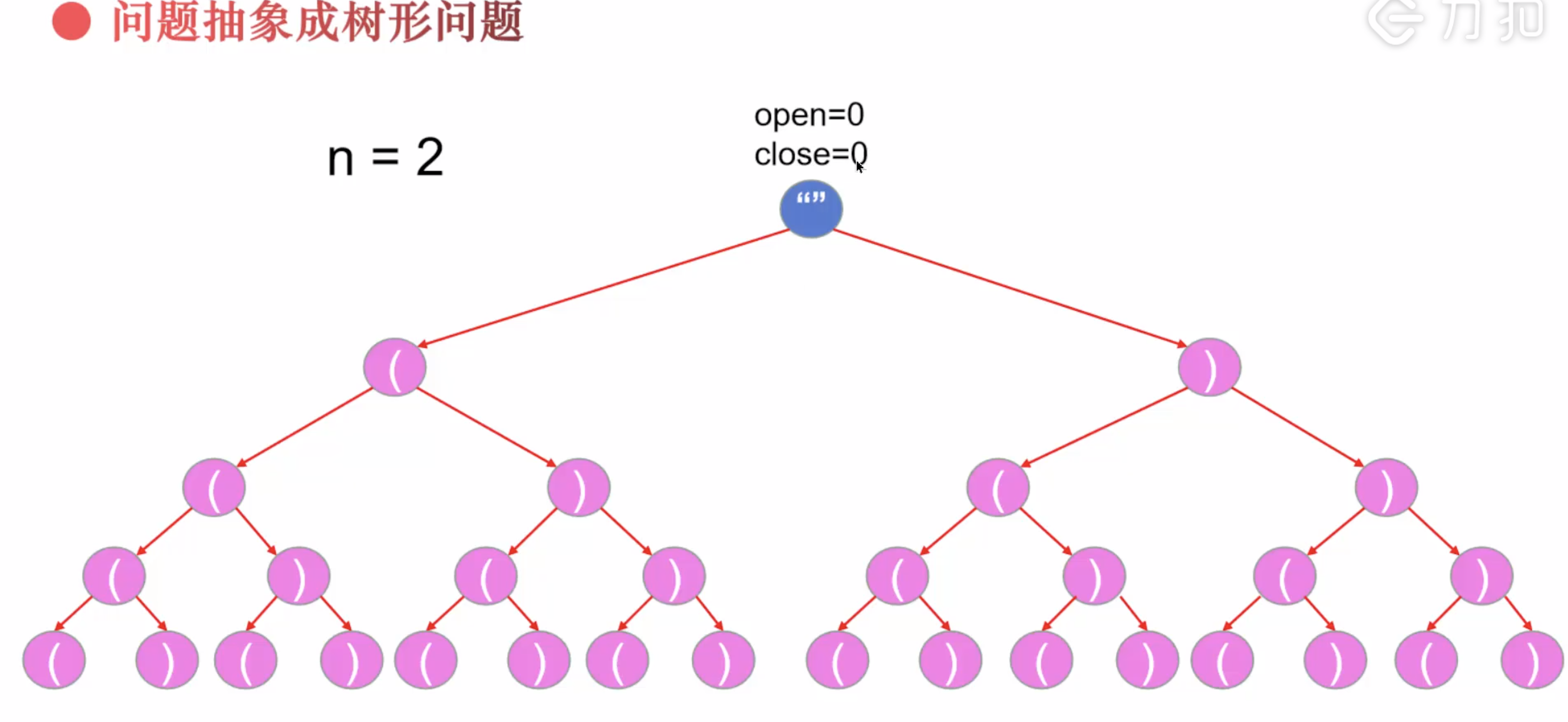
然后对🌲进行剪枝

剪枝标准

• 右括号数量大于左括号(其中就包括了开头是右括号的情况)
• 左括号数量大于n的值

终止条件，字符串长度等于2 * n

var generateParenthesis = function(n) {
  const dfs = (path, open, close) => {
    if(close > open || open > n) return false

    if(path.length === 2 * n) {
      res.push(path)
      return res
    }
    dfs(path + '(', open + 1, close)
    dfs(path + ')', open, close + 1)
  }
  const res = []
  dfs('', 0, 0)
  return res 
};

lc79. 矩阵中的路径/单词搜索中等hot

题目描述

给定一个 m x n 二维字符网格 board 和一个字符串单词 word。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

例如，在下面的 3×4 的矩阵中包含单词 "ABCCED"（单词中的字母已标出）。

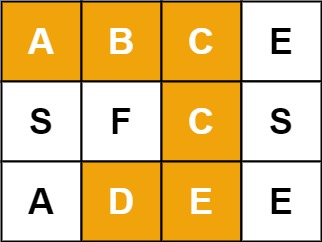
示例 1：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

输入：board = [["a","b"],["c","d"]], word = "abcd"
输出：false

思路： DFS

1. 遍历整个网格，每个字符都尝试作为单词的起点。
2. 对于每个起点，尝试以 DFS 方式 向上下左右扩展搜索。
3. 进入下一个格子时要标记访问状态，避免重复访问。
4. 如果某条路径不通（剪枝），就回溯（恢复现场）继续尝试其他路径。

var exist = function(board, word) {
  const m = board.length;
  const n = board[0].length;

  const dfs = (i, j, k) => {
    // 越界 或 字符不匹配
    if (i < 0 || i >= m || j < 0 || j >= n || board[i][j] !== word[k]) {
      return false;
    }
    // 所有字符匹配完毕
    if (k === word.length - 1) return true;

    const temp = board[i][j];
    board[i][j] = '#'; // 标记为已访问

    const res = dfs(i + 1, j, k + 1) ||
                dfs(i - 1, j, k + 1) ||
                dfs(i, j + 1, k + 1) ||
                dfs(i, j - 1, k + 1);

    board[i][j] = temp; // 恢复现场
    return res;
  };

  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (dfs(i, j, 0)) return true;
    }
  }

  return false;
};

M,N 分别为矩阵行列大小， K 为字符串 word 长度。

时间复杂度O(3^K * MN) 最差情况下，需要遍历矩阵中长度为 K 字符串的所有方案，时间复杂度为 O(3^K) 矩阵中共有 MN 个起点，时间复杂度为 O(MN) 方案数计算： 设字符串长度为 K ，搜索中每个字符有上、下、左、右四个方向可以选择，舍弃回头（上个字符）的方向，剩下 3 种选择，因此方案数的复杂度为 O(3^K)

空间复杂度 O(K) ： 搜索过程中的递归深度不超过 K ，因此系统因函数调用累计使用的栈空间占用 O(K) 最坏情况下 K = MN，递归深度为 MN ，此时系统栈使用 O(MN)的额外空间

39. 组合总和/两数之和回溯中等hot

题目描述

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

思路

标准的回溯模版

var combinationSum = function(candidates, target) {
  candidates.sort((a, b) => a - b)
  const res = []

  const dfs = (start, temp, track) => {
    if(temp === target) {
      res.push([...track])
      return
    }

    for(let i = start; i < candidates.length; i++) {
      if(temp + candidates[i] <= target) {
        temp += candidates[i]
        track.push(candidates[i])
        dfs(i, temp, track)
        track.pop()
        temp -= candidates[i]
      }
    }
  }
  dfs(0, 0, [])
  return res
};

时间复杂度:O(n)

空间复杂度:O(n)，最坏O(target)

加起来和为目标值的组合(二)中等

题目描述

给出一组候选数 c 和一个目标数 t ，找出候选数中起来和等于 t 的所有组合。

c 中的每个数字在一个组合中只能使用一次。

注意：

1. 题目中所有的数字（包括目标数 t ）都是正整数
2. 组合中的数组递增
3. 结果中不能包含重复的组合
4. 组合之间的排序按照索引从小到大依次比较，小的排在前面，如果索引相同的情况下数值相同，则比较下一个索引。

要求：空间复杂度 O(n!) ， 时间复杂度 O(n!)

示例1

输入：[100,10,20,70,60,10,50],80

返回值：[[10,10,60],[10,20,50],[10,70],[20,60]]

说明：给定的候选数集是[100,10,20,70,60,10,50]，目标数是80   

示例2

输入：[2],1

返回值：[]

思路

function combinationSum2( num ,  target ) {
    // write code here
  	// 对原数组排序
    num.sort((a, b) => a - b)
    const temp = [], res = []
    dfs(num, target, 0, temp, res, 0)
    return res
}

function dfs(num, target, temp,tempArr, res, start) {
  	// 遍历的元素的累加值
    if(temp === target) {
        res.push([...tempArr])
        return
    }
  	// 越界
    if(start >= num.length) return
    
    for(let i = start; i < num.length; i++) {
        // 去重
        if(i > start && num[i] === num[i - 1]) continue

        if(temp + num[i] <= target) {
            temp += num[i]
            tempArr.push(num[i])
            dfs(num, target, temp, tempArr, res, i + 1)
            // 回溯 撤销操作
            tempArr.pop()
            temp -= num[i]
        }
    }
}

时间复杂度:O(n)

空间复杂度:O(n)

lc17. 电话号码的字母组合中等

题目描述

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

思路：dfs + 回溯

这道题有暴力法可以解，但是要嵌套三次循环，采用dfs可以降时间复杂度

function letterCombinations(digits) {
  if (!digits.length) return [];

  const map = {
    '2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl',
    '6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'
  };

  const res = [];

  function backtrack(index, path) {
    if (index === digits.length) {
      res.push(path);
      return;
    }

    const letters = map[digits[index]];
    for (let letter of letters) {
      backtrack(index + 1, path + letter);
    }
  }

  backtrack(0, '');
  return res;
}

时间复杂度： 每个数字对应 3~4 个字母，最长输入长度为 n，组合总数约为 O(4^n)，即每个位置最多 4 种选择。

空间复杂度： 递归栈深度为 n，加上结果数组，空间复杂度约为 O(n * 4^n)。

lc38. 外观数列中等

题目描述

给定一个正整数 n ，输出外观数列的第 n 项。

「外观数列」是一个整数序列，从数字 1 开始，序列中的每一项都是对前一项的描述。

你可以将其视作是由递归公式定义的数字字符串序列：

• countAndSay(1) = "1"
• countAndSay(n) 是对 countAndSay(n-1) 的描述，然后转换成另一个数字字符串。

前五项如下：

1.     1
2.     11
3.     21
4.     1211
5.     111221
第一项是数字 1 
描述前一项，这个数是 1 即 “ 一 个 1 ”，记作 "11"
描述前一项，这个数是 11 即 “ 二 个 1 ” ，记作 "21"
描述前一项，这个数是 21 即 “ 一 个 2 + 一 个 1 ” ，记作 "1211"
描述前一项，这个数是 1211 即 “ 一 个 1 + 一 个 2 + 二 个 1 ” ，记作 "111221"

要 描述 一个数字字符串，首先要将字符串分割为 最小 数量的组，每个组都由连续的最多 相同字符 组成。然后对于每个组，先描述字符的数量，然后描述字符，形成一个描述组。要将描述转换为数字字符串，先将每组中的字符数量用数字替换，再将所有描述组连接起来。

例如，数字字符串 "3322251" 的描述如下图：

示例 1：

输入：n = 1
输出："1"
解释：这是一个基本样例。

示例 2：

输入：n = 4
输出："1211"
解释：
countAndSay(1) = "1"
countAndSay(2) = 读 "1" = 一 个 1 = "11"
countAndSay(3) = 读 "11" = 二 个 1 = "21"
countAndSay(4) = 读 "21" = 一 个 2 + 一 个 1 = "12" + "11" = "1211"

思路

很简单的一道递归题

var countAndSay = function(n) {
  if(n === 1) return '1'
  let pre = countAndSay(n - 1)

  let str = '', left = 0, right = 0
  while(right < pre.length) {
    while(pre[left] === pre[right] && right < pre.length) right++

    str += (String(right - left) + pre[left])
    left = right
  }

  return str
};

时间复杂度:O(n)

空间复杂度:O(n) 每层递归都创建pre存储f(n - 1)

思路二：滚动数组

用pre代替f(n - 1)降低空间复杂度

var countAndSay = function(n) {
  let pre = '1', str = '1'
  for(let i = 1; i < n; i++) {
    pre = str
    str = ''
    let left = 0, right = 0
    while(right < pre.length) {
      while(pre[left] === pre[right] && right < pre.length) right++

      str += (String(right - left) + pre[left])
      left = right
    }
  }
  return str
};

时间复杂度:O(n)

空间复杂度:O(1)

lc131. 分割回文串中等

题目描述

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

输入：s = "a"
输出：[["a"]]

思路

标准回溯

回溯搜索所有切割路径

• 从头开始枚举每个位置 i，判断 s[start:i+1] 是否是回文。
  • 是：就把这段加入 path，继续 dfs。
  • 否：跳过。
• 递归终止条件：切到了末尾（start === s.length），把当前路径加入结果。

var partition = function(s) {
  var res = [], path = []
  var backTrack = (start) => {
      if (start > s.length) return false
      if (start === s.length) {
          res.push(path.slice())
          return false
      }
      for (let i = start; i < s.length; i ++) {
          if(isValid(s, start, i)) {
              var str = s.substr(start, i - start + 1);
              path.push(str)
              backTrack(i + 1)
              path.pop()
          }
      }
  }
  backTrack(0)
  return res
};
// 双指针判断回文串
var isValid = (str, start, end) => {
  for(let i = start, j = end; i < j; i ++, j--) {
      if (str[i] !== str[j]) return false
  }
  return true
}

51. N 皇后困难hot

题目描述

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

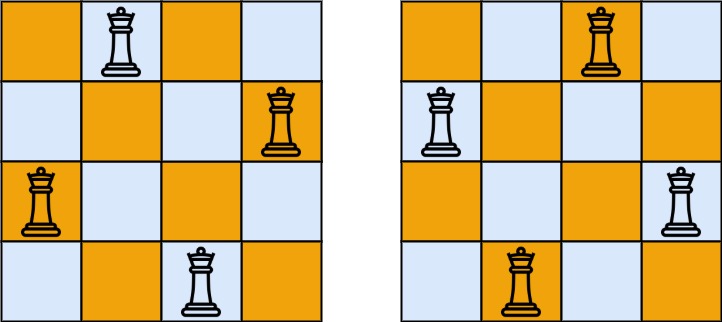
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

思路

不能在同一行 同一列 或同一条斜线上

var solveNQueens = function(n) {
  function isValid(row, col, chessBoard, n) {
    //不用判断同一行的因为回溯就是在同一行不同列放置皇后
    for(let i = 0; i < row; i++) {
      // 同一列的判断
      if(chessBoard[i][col] === 'Q') {
        return false
      }
    }
    for(let i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
      // 135度斜角判断 左上斜线 不需要判断下面的
      if(chessBoard[i][j] === 'Q') {
        return false
      }
    }
      // 45度斜角判断 右上斜线 不需要判断下面的
    for(let i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
      if(chessBoard[i][j] === 'Q') {
        return false
      }
    }
    return true
  }

  function transformChessBoard(chessBoard) {
    // 转换一下输出
    let chessBoardBack = []
    chessBoard.forEach(row => {
      let rowStr = ''
      row.forEach(value => {
        rowStr += value
      })
      chessBoardBack.push(rowStr)
    })

    return chessBoardBack
  }

    let result = []
    function backtracing(row,chessBoard) {
      if(row === n) {
        // 最后一行 能放下了就已经算成功了
        result.push(transformChessBoard(chessBoard))
        return
      }
      for(let col = 0; col < n; col++) {
        // 遍历列 回溯行
        if(isValid(row, col, chessBoard, n)) {
          chessBoard[row][col] = 'Q'
          backtracing(row + 1,chessBoard)
          chessBoard[row][col] = '.'
        }
      }
    }
    let chessBoard = Array.from(new Array(n), ()=> new Array(n).fill('.'))
    backtracing(0,chessBoard)
    return result
};

一个数从 1 开始，每一步只能乘 3 或加 5，目标值为 1024，写代码找出一种解法或所有解法。

function findPathToTarget(target: number): number[] | null {
  const queue: [number, number[]][] = [[1, [1]]];
  const visited = new Set<number>();

  while (queue.length > 0) {
    const [current, path] = queue.shift()!;

    if (current === target) return path;
    if (current > target || visited.has(current)) continue;

    visited.add(current);

    queue.push([current * 3, [...path, current * 3]]);
    queue.push([current + 5, [...path, current + 5]]);
  }

  return null; // No path found
}

const result = findPathToTarget(1024);
console.log(result);