小宋爱睡觉
  • 数组
Crucials
2022-02-07

数学问题

# 数学问题

# lc136. 只出现一次的数字简单

题目描述

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,1]
输出: 1
1
2

示例 2:

输入: [4,1,2,1,2]
输出: 4
1
2

思路

这道题要求不用额外空间实现，那就是使用异或

  • 任何数和自己做异或运算，结果为 0，即a⊕a=0。
  • 任何数和0 做异或运算，结果还是自己，即 a⊕0=a。
  • 异或运算中，满足交换律和结合律，也就是a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b
var singleNumber = function(nums) {
  let init = nums[0];
  for(let i = 1; i < nums.length; i++){
      init ^=  nums[i];
  }
  return init;
};
1
2
3
4
5
6
7

# lc191. 位1的个数简单

题目描述

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 '1' 的个数（也被称为汉明重量 (opens new window)）。

示例 1：

输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 '1'。
1
2
3

示例 2：

输入：00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 '1'。
1
2
3

示例 3：

输入：11111111111111111111111111111101
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 '1'。
1
2
3

提示：

  • 输入必须是长度为 32 的 二进制串 。

进阶：

  • 如果多次调用这个函数，你将如何优化你的算法？

思路

首先介绍一下&运算符

直接上🌰

console.log(12 & 5); //返回值4

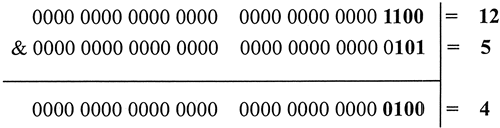
|运算符

console.log(12 | 5); //返回值13

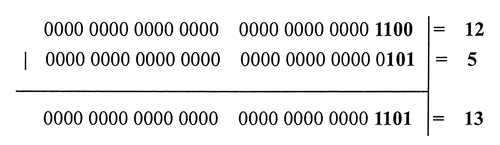
很明显 & 是与 ｜是或

var hammingWeight = function(n) {
    let count = 0
    while(n) {
      n &= n - 1
      count++
    }
    return count
};
1
2
3
4
5
6
7
8

# lc283. 移动零简单hot

题目描述

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例:

输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
1
2

思路：双指针

用i表示当前不为0的数，j表示当前为0的数，i先走，遇到不为0的数就和前面的j进行互换,这样0就到最后去了

var moveZeroes = function(nums) {
  let i = 0, j = 0
  while(i < nums.length) {
    if(nums[i] !== 0) {
      [nums[i], nums[j]] = [nums[j], nums[i]]
      j++
    }

    i++
  }
};
1
2
3
4
5
6
7
8
9
10
11

# lc118. 杨辉三角简单

题目描述

给定一个非负整数 *numRows，*生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

img

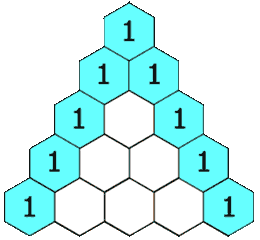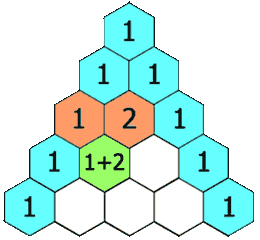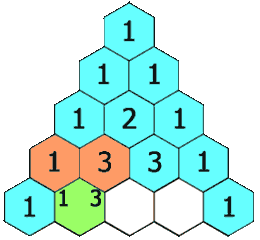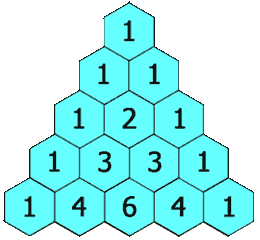
示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
1
2

示例 2:

输入: numRows = 1
输出: [[1]]
1
2

思路

常规思路

var generate = function(numRows) {
  if(!numRows) return []
  const arr = new Array()
  for(let i = 0; i < numRows; i++){
    arr[i] = new Array()
    arr[i][0] = 1; arr[i][i] = 1;
      for(let j = 1; j < i; j++){
      arr[i][j] = arr[i-1][j-1] + arr[i-1][j] 
    }
  }
  return arr
};
1
2
3
4
5
6
7
8
9
10
11
12

# lc66. 加一简单

题目描述

给定一个由 整数 组成的 非空 数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位， 数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例 1：

输入：digits = [1,2,3]
输出：[1,2,4]
解释：输入数组表示数字 123。
1
2
3

示例 2：

输入：digits = [4,3,2,1]
输出：[4,3,2,2]
解释：输入数组表示数字 4321。
1
2
3

示例 3：

输入：digits = [0]
输出：[1]
1
2

思路

很简单，跟两数相加一样

var plusOne = function(digits) {
  let car = 1
  let sum = 0
  for(let i = digits.length - 1; i >= 0; i--) {
    if(car) {
      sum = digits[i] + car
      digits[i] = sum % 10
      car = Math.floor(sum / 10)
    } else {
      break
    }
  }
  if(car) digits.unshift(car)
  return digits
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

时间复杂度:O(n)

空间复杂度:O(1)

# lc268. 丢失的数字简单

题目描述

给定一个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数。

示例 1：

输入：nums = [3,0,1]
输出：2
解释：n = 3，因为有 3 个数字，所以所有的数字都在范围 [0,3] 内。2 是丢失的数字，因为它没有出现在 nums 中。
1
2
3

示例 2：

输入：nums = [0,1]
输出：2
解释：n = 2，因为有 2 个数字，所以所有的数字都在范围 [0,2] 内。2 是丢失的数字，因为它没有出现在 nums 中。
1
2
3

示例 3：

输入：nums = [9,6,4,2,3,5,7,0,1]
输出：8
解释：n = 9，因为有 9 个数字，所以所有的数字都在范围 [0,9] 内。8 是丢失的数字，因为它没有出现在 nums 中。
1
2
3

示例 4：

输入：nums = [0]
输出：1
解释：n = 1，因为有 1 个数字，所以所有的数字都在范围 [0,1] 内。1 是丢失的数字，因为它没有出现在 nums 中。
1
2
3

思路

直接上代码，等差数列求和然后依次减去数组每一项的值，剩下的就是丢失的那个数字

var missingNumber = function(nums) {
  let len = nums.length
  let sum = (len + 1) * len / 2
  for(let i = 0; i < len; i++) {
    sum -= nums[i]
  }
  return sum
};
1
2
3
4
5
6
7
8

# lc326. 3 的幂简单

题目描述

给定一个整数，写一个函数来判断它是否是 3 的幂次方。如果是，返回 true ；否则，返回 false 。

整数 n 是 3 的幂次方需满足：存在整数 x 使得 n == 3x

示例 1：

输入：n = 27
输出：true
1
2

示例 2：

输入：n = 0
输出：false
1
2

示例 3：

输入：n = 9
输出：true
1
2

示例 4：

输入：n = 45
输出：false
1
2
var isPowerOfThree = function(n) {
  while(n >= 3) {
    n = n / 3
  }

  return n === 1
};
1
2
3
4
5
6
7

# lc7. 整数反转中等

题目描述

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。

如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ，就返回 0。

假设环境不允许存储 64 位整数（有符号或无符号）。

示例 1：

输入：x = 123
输出：321
1
2

示例 2：

输入：x = -123
输出：-321
1
2

示例 3：

输入：x = 120
输出：21
1
2

示例 4：

输入：x = 0
输出：0
1
2

法一：字符串拼接

var reverse = function(x) {
  if(x === 0) return 0
  else if(x > 0) {
    let str = String(x)
    let res = Number(str.split('').reverse().join(''))
    return res > Math.pow(2, 31) - 1 ? 0 : res
  } else {
    let str = String(x).slice(1)
    let res = Number(`-${str.split('').reverse().join('')}`)
    return res < Math.pow(-2, 31) ? 0 : res
  }
};
1
2
3
4
5
6
7
8
9
10
11
12

法二

  • 声明一个变量ret存放结果

  • 用x % 10获取最后一个数

  • ret每次加上他自身乘以10 和 最后一个数，也就相当于取原来数字的最后一位拼接到新数字的最后面

var reverse = function(x) {
    let ret = 0;
    while(x){
        ret = ret * 10 + x % 10;
        if(ret > Math.pow(2, 31) - 1 || ret < Math.pow(-2, 31)) return 0;
        x = (x / 10) | 0
    }
    return ret
};
1
2
3
4
5
6
7
8
9

# lc166. 分数到小数中等

题目描述

给定两个整数，分别表示分数的分子 numerator 和分母 denominator，以 字符串形式返回小数 。

如果小数部分为循环小数，则将循环的部分括在括号内。

如果存在多个答案，只需返回 任意一个 。

对于所有给定的输入，保证 答案字符串的长度小于 104 。

示例 1：

输入：numerator = 1, denominator = 2
输出："0.5"
1
2

示例 2：

输入：numerator = 2, denominator = 1
输出："2"
1
2

示例 3：

输入：numerator = 2, denominator = 3
输出："0.(6)"
1
2

示例 4：

输入：numerator = 4, denominator = 333
输出："0.(012)"
1
2

示例 5：

输入：numerator = 1, denominator = 5
输出："0.2"
1
2

思路

小数部分乘以10 继续除

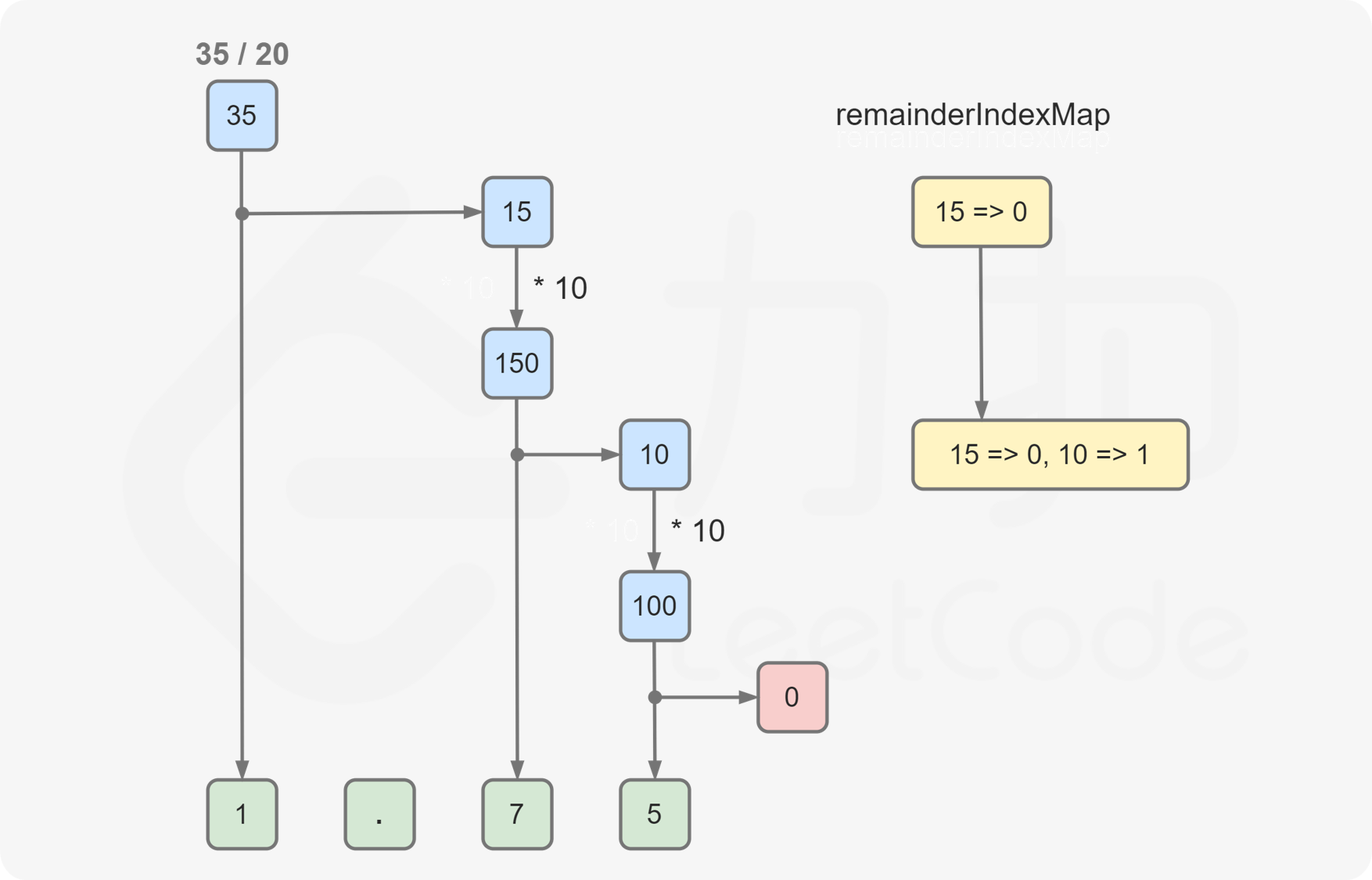
var fractionToDecimal = function(numerator, denominator) {
  if(numerator % denominator === 0) return String(Math.floor(numerator / denominator))
  const res = []
  if((numerator < 0 && denominator > 0) || (numerator > 0 && denominator < 0)) res.push('-')

  numerator = Math.abs(numerator)
  denominator = Math.abs(denominator)
  // interger
  res.push(Math.floor(numerator / denominator), '.')

  // fraction
  const fractionPart = [];
  const map = new Map();
    let remainder = numerator % denominator;
    let index = 0;
    while (remainder !== 0 && !map.has(remainder)) {
        map.set(remainder, index);
        remainder *= 10;
        fractionPart.push(Math.floor(remainder / denominator));
        remainder %= denominator;
        index++;
    }
    if (remainder !== 0) { // 有循环节
        let insertIndex = map.get(remainder);
        fractionPart.splice(insertIndex, 0, '(');
        fractionPart.push(')');
    }
    res.push(fractionPart.join(''));

    return res.join('');
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

时间复杂度:O(n)

空间复杂度:O(n)

# 414. 第三大的数简单hot

题目描述

给你一个非空数组，返回此数组中 第三大的数 。如果不存在，则返回数组中最大的数。

示例 1：

输入：[3, 2, 1]
输出：1
解释：第三大的数是 1 。
1
2
3

示例 2：

输入：[1, 2]
输出：2
解释：第三大的数不存在, 所以返回最大的数 2 。
1
2
3

示例 3：

输入：[2, 2, 3, 1]
输出：1
解释：注意，要求返回第三大的数，是指在所有不同数字中排第三大的数。
此例中存在两个值为 2 的数，它们都排第二。在所有不同数字中排第三大的数为 1 。
1
2
3
4
var thirdMax = function (nums) {
  let temp = Array.from(new Set(nums)).sort((a, b) => {
    return b - a
  })
  let len = temp.length
  if (len < 3) {
    return temp[0]
  }
  return temp[2]
};
1
2
3
4
5
6
7
8
9
10

# 498. 对角线遍历中等hot

题目描述

给你一个大小为 m x n 的矩阵 mat ，请以对角线遍历的顺序，用一个数组返回这个矩阵中的所有元素。

示例 1：

img

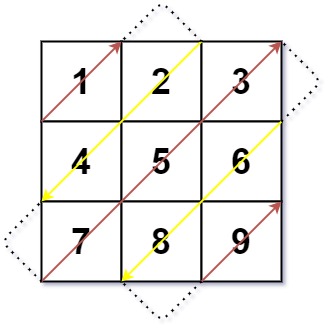
输入：mat = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,4,7,5,3,6,8,9]
1
2

示例 2：

输入：mat = [[1,2],[3,4]]
输出：[1,2,3,4]
1
2

思路

声明一个map，由于是对角线进行遍历，所以有i + j都是相等的，然后最后看看是否2的倍数，不是的话就原样输出，是就reverse

var findDiagonalOrder = function(mat) {
  const row = mat.length
  const col = mat[0].length
  const record = new Map()
  for (let i = 0; i < row; i++) {
    for (let j = 0; j < col; j++) {
      const key = i + j
      if (!record.has(key)) record.set(key, [])
      record.get(key).push(mat[i][j])
    }
  }
  const res = []
  for (const [key, nums] of record.entries()) {
    key % 2 === 1 ? res.push(...nums) : res.push(...nums.reverse())
  }
  return res
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

时间复杂度:O(n)

空间复杂度:O(n)

上次更新: 2022/03/20, 19:40:28
TopK
拓扑排序

← 拓扑排序→

Copyright © 2021-2022 粤ICP备2021165371号