lc20. 求有效的括号 简单hot

题目描述

给定一个只包括'('，')'，'{'，'}'，'['，']'的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。

示例：

输入：s = "()"
输出：true

输入：s = "()[]{}"
输出：true

输入：s = "([)]"
输出：false

输入：s = "{[]}"
输出：true

思路：

借助了map数据结构，同时用了栈的思想，新增一个stackArr的数组，通过循环遍历输入字符串判断：

如果输入字符串在Map中存在（正括号存在即合理），继续循环

• 如果不存在，再获取缓存中最后一项的值进行配对～配对成功即合理、移除当前缓存

• 继续循环直到遍历完成

• 遍历完成后如果缓存中仍有数据、说明有正括号未匹配结果，则return false，反之return true

var isValid = function(s) {
    const stackArr = []
    const map = new Map()
    map.set('(', ')')
    map.set('{', '}')
    map.set('[', ']')
    for(let i = 0; i < s.length; i++) {
        if(map.has(s[i])) stackArr.push(s[i])
        else {
            if(stackArr.length === 0) return false
            if (map.get(stackArr[stackArr.length - 1]) === s[i]) stackArr.pop()
            else return false
        }
    }
    if(stackArr.length) return false
    return true
};

时间复杂度: O(n)

空间复杂度: O(n)

lc32. 最长有效括号困难hot

题目描述

给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

示例 1：

输入：s = "(()"
输出：2
解释：最长有效括号子串是 "()"

示例 2：

输入：s = ")()())"
输出：4
解释：最长有效括号子串是 "()()"

示例 3：

输入：s = ""
输出：0

思路

初始化一个栈，初始入栈 -1，表示“最后一个不匹配的位置”。

遍历字符串：

• 如果是 '('，将当前下标 i 入栈。
• 如果是 ')'：
  • 弹出栈顶元素，表示匹配一个 '('。
  • 若栈为空，说明当前 ')' 没有匹配，将当前索引 i 入栈作为新的基准。
  • 若栈不为空，则当前有效长度为 i - 栈顶元素索引，更新最大值。

function longestValidParentheses(s) {
  const stack = [-1]; // 初始化栈
  let maxLen = 0;

  for (let i = 0; i < s.length; i++) {
    if (s[i] === '(') {
      stack.push(i);
    } else {
      stack.pop(); // 弹出一个 '(' 或 -1

      if (stack.length === 0) {
        stack.push(i); // 作为新的 base 起点
      } else {
        maxLen = Math.max(maxLen, i - stack[stack.length - 1]);
      }
    }
  }
  return maxLen;
}

时间复杂度: O(n)

空间复杂度: O(n)

前后同时遍历

用两个计数器 left 和 right 。

从左到右遍历字符串，遇到(，我们增加left 计数器，对于遇到的每个 ) ，我们增加 right 计数器。每当 left 计数器与 right 计数器相等时，我们计算当前有效字符串的长度，并且记录目前为止找到的最长子字符串。当 right 计数器比 left 计数器大时，我们将 left 和 right 计数器同时变回 0。

这样的做法贪心地考虑了以当前字符下标结尾的有效括号长度，每次当右括号数量多于左括号数量的时候之前的字符我们都扔掉不再考虑，重新从下一个字符开始计算，但这样会漏掉一种情况，就是遍历的时候左括号的数量始终大于右括号的数量，即 (() ，这种时候最长有效括号是求不出来的。

解决的方法也很简单，我们只需要从右往左遍历用类似的方法计算即可，只是这个时候判断条件反了过来：

当 left 计数器比 right 计数器大时，我们将 left 和 right 计数器同时变回 0 当 left 计数器与 right 计数器相等时，我们计算当前有效字符串的长度，并且记录目前为止找到的最长子字符串

var longestValidParentheses = function(s) {
  let left = 0, right = 0, maxlength = 0;
  for (let i = 0; i < s.length; i++) {
      if (s[i] === '(') {
        left++;
      } else {
        right++;
      }
      if (left === right) {
        maxlength = Math.max(maxlength, 2 * right);
      } else if (right > left) {
        left = right = 0;
      }
  }
  left = right = 0;
  for (let i = s.length - 1; i >= 0; i--) {
      if (s[i] === '(') {
        left++;
      } else {
        right++;
      }
      if (left === right) {
        maxlength = Math.max(maxlength, 2 * left);
      } else if (left > right) {
        left = right = 0;
      }
  }
  return maxlength;
};

时间复杂度: O(n)

空间复杂度: O(1)

lc. 1047删除字符串中的相邻重复项简单

题目描述

给出由小写字母组成的字符串S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入："abbaca"
输出："ca"
解释：
例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同
这是此时唯一可以执行删除操作的重复项。
之后我们得到字符串 "aaca"
其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

思路：

我们都刷了这么多题了，第一反应肯定是用栈弹出的形式来匹配是否相同的

• 那么我们可以维护一个栈数组

• 如果栈顶元素与将要入栈的元素相同的话

• 那么栈顶元素出栈

很简单是不是

时间复杂度O(n)

空间复杂度O(n)

var removeDuplicates = function(s) {
    const stack = []
    // 发现新大陆 ！字符串也可以用for .. of..
    for(c of s) {
        let temp = stack.pop()
        if(c !== temp) {
            stack.push(temp)
            stack.push(c)
        }
    }
    return stack.join('')
};

这里奇奇怪怪的，时间复杂度为O(n) 但是跑了几次都只击败了10%左右的用户，莫非还有O(1)的空间复杂度，暂时没找到，先mark一下

lc1209. 删除字符串中的相邻重复项中等

题目描述：

给你一个字符串 s，「k倍重复项删除操作」将会从 s 中选择 k 个相邻且相等的字母，并删除它们，使被删去的字符串的左侧和右侧连在一起。

你需要对 s 重复进行无限次这样的删除操作，直到无法继续为止。

在执行完所有删除操作后，返回最终得到的字符串。

本题答案保证唯一。

示例 1：

输入：s = "abcd", k = 2
输出："abcd"
解释：没有要删除的内容。

示例 2：

输入：s = "deeedbbcccbdaa", k = 3
输出："aa"
解释： 
先删除 "eee" 和 "ccc"，得到 "ddbbbdaa"
再删除 "bbb"，得到 "dddaa"
最后删除 "ddd"，得到 "aa"

示例 3：

输入：s = "pbbcggttciiippooaais", k = 2
输出："ps"

法一：把进栈的字母相同 改为 合并为同一个元素

• 每次入栈元素和栈顶元素匹配
• 注意栈顶元素可能不只是一个字母

  • 如果栈顶元素的第一位和入栈元素不相同

    • 准备入栈的元素执行入栈操作

  • 如果栈顶元素的第一位和入栈元素相同

    • 判断一下栈顶元素长度是不是等于k - 1(因为等于k - 1的话加上这个入栈元素就是k位，那么就可以出栈了)
    • 等于栈顶元素就出栈
    • 不等于就把栈顶元素和入栈元素拼接起来 然后重新替换原来的栈顶元素 执行入栈

时间复杂度O(n)

空间复杂度O(n)

var removeDuplicates = function(s, k) {
    const stack = []
    for(let c of s) {
        const prev = stack.pop()
        if(!prev || c !== prev[0]) {
            stack.push(prev)
            stack.push(c)
        } else if(prev.length < k - 1) {
            stack.push(prev + c)
        }
    }
    return stack.join('')
};

法二 维护一个计算次数的栈和储存元素的栈

• 执行一遍循环

• 如果入栈元素和栈顶元素相同

  • 数字栈的栈顶元素加一
  • 如果累积到k了 储存元素的栈执行k次出栈

• 如果入栈元素和栈顶元素不同

  • 那么入栈元素入储存元素的栈 数字栈推入一个为1的元素

时间复杂度O(n)

空间复杂度O(n)

var removeDuplicates = function (s, k) {
    let stack = [] //字母栈
    let countStack = [] //数字栈
    let i = 0
    while(i < s.length){
        if(stack[stack.length - 1] == s[i]){
            stack.push(s[i])
            countStack[countStack.length-1] +=   1
            if(countStack[countStack.length-1] == k){
                for(let j = 0; j < k; j++){ 
                    //字母栈出栈
                    stack.pop()
                }
                countStack.pop() //数字栈出栈
            }
        }else{
            stack.push(s[i])
            countStack.push(1)
        }
        i++
    }
    return stack.join('')
};

这里很奇怪的是两种方法都是时间复杂度O(n) 空间复杂度O(n) 但是执行用时却有很大的差别，有待考究

lc150. 逆波兰表达式求值中等

题目描述

根据 逆波兰表示法 (opens new window)，求表达式的值。

有效的算符包括 +、-、*、/ 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

注意 两个整数之间的除法只保留整数部分。

可以保证给定的逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

var evalRPN = function(tokens) {
  let methods = ['+', '-', '*', '/']
  const stack = []
  for(let item of tokens) {
    if(!methods.includes(item)) stack.push(+item)
    else {
      let num2 = stack.pop()
      let num1 = stack.pop()
      switch(item) {
        case '+':
          stack.push(num1 + num2)
          break
        case '-':
          stack.push(num1 - num2)
          break
        case '*':
          stack.push(num1 * num2)
          break
        case '/':
          stack.push(Math.trunc(num1 / num2))
          break
      }
    }
  }
  return stack[0]
};

lc155. 最小栈简单

题目描述

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

• push(x) —— 将元素 x 推入栈中。
• pop() —— 删除栈顶的元素。
• top() —— 获取栈顶元素。
• getMin() —— 检索栈中的最小元素。

示例:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

class MinStack {
  private stack: number[] = [];
  private minStack: number[] = [];

  push(x: number): void {
    this.stack.push(x);
    const min = this.minStack.length === 0 
      ? x 
      : Math.min(x, this.minStack[this.minStack.length - 1]);
    this.minStack.push(min);
  }

  pop(): void {
    this.stack.pop();
    this.minStack.pop();
  }

  top(): number {
    return this.stack[this.stack.length - 1];
  }

  getMin(): number {
    return this.minStack[this.minStack.length - 1];
  }
}

lc225. 用队列实现栈

题目描述

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

• void push(int x) 将元素 x 压入栈顶。
• int pop() 移除并返回栈顶元素。
• int top() 返回栈顶元素。
• boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

• 你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
• 你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

思路

尽量不要出现pop()

/**
 * Initialize your data structure here.
 */
var MyStack = function() {
    this.queue1 = [];
    this.queue2 = [];
};
// 
// 
/**
 * Push element x onto stack. 
 * @param {number} x
 * @return {void}
 */


MyStack.prototype.push = function(x) {
    this.queue2.push(x);
    while (this.queue1.length) this.queue2.push(this.queue1.shift());
    [this.queue1, this.queue2] = [this.queue2, this.queue1];
};

/**
 * Removes the element on top of the stack and returns that element.
 * @return {number}
 */
MyStack.prototype.pop = function() {
    return this.queue1.shift();
};

/**
 * Get the top element.
 * @return {number}
 */
MyStack.prototype.top = function() {
    return this.queue1[0];
};

/**
 * Returns whether the stack is empty.
 * @return {boolean}
 */
MyStack.prototype.empty = function() {
    return !this.queue1.length;
};

/**
 * Your MyStack object will be instantiated and called as such:
 * var obj = new MyStack()
 * obj.push(x)
 * var param_2 = obj.pop()
 * var param_3 = obj.top()
 * var param_4 = obj.empty()
 */

单调栈

lc739. 每日温度中等hot

题目描述

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指在第 i 天之后，才会有更高的温度。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例 1:

输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

示例 2:

输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]

示例 3:

输入: temperatures = [30,60,90]
输出: [1,1,0]

思路

我们用一个栈来「记录还没找到答案的温度的索引」。

并且我们规定：

栈中温度对应的索引，按照温度 从高到底排序（栈顶是最低的）。

这样做的关键在于：

• 每次有一个新的更高温度时，就可以「一次性解决」一堆低温度的问题！

类比：我们拿信等通知

你可以想象成，每个温度是一个「发起请求等通知的人」，比如：

第 i 天温度是 71，它说：「我想知道啥时候天气会升温！」

• 我们把它放进栈里（它在等通知）
• 接下来的日子气温变成 72 了，它会通知前面等着的 71，说「你等的来了！我比你高！」

于是我们就知道：

answer[71那天] = 今天 - 它那天

var dailyTemperatures = function(temperatures) {
  const len = temperatures.length
  const res = new Array(len).fill(0)
  const stack = []
  for(let i = 0; i < len; i++) {
    while(stack.length && temperatures[stack[stack.length - 1]] < temperatures[i]) {
      let index = stack.pop()
      res[index] = i - index
    }
    stack.push(i)
  }
  return res
};

时间复杂度：O(n)，其中 n 是温度列表的长度。正向遍历温度列表一遍，对于温度列表中的每个下标，最多有一次进栈和出栈的操作。

空间复杂度：O(n)，其中 n 是温度列表的长度。需要维护一个单调栈存储温度列表中的下标。

lc402. 移除掉k位数字中等

题目描述

给你一个以字符串表示的非负整数 num 和一个整数 k ，移除这个数中的k 位数字，使得剩下的数字最小。请你以字符串形式返回这个最小的数字。

示例 1 ：

输入：num = "1432219", k = 3
输出："1219"
解释：移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219 。

示例 2 ：

输入：num = "10200", k = 1
输出："200"
解释：移掉首位的 1 剩下的数字为 200. 注意输出不能有任何前导零。

示例 3 ：

输入：num = "10", k = 2
输出："0"
解释：从原数字移除所有的数字，剩余为空就是 0 。

思路: 利用单调栈

/**
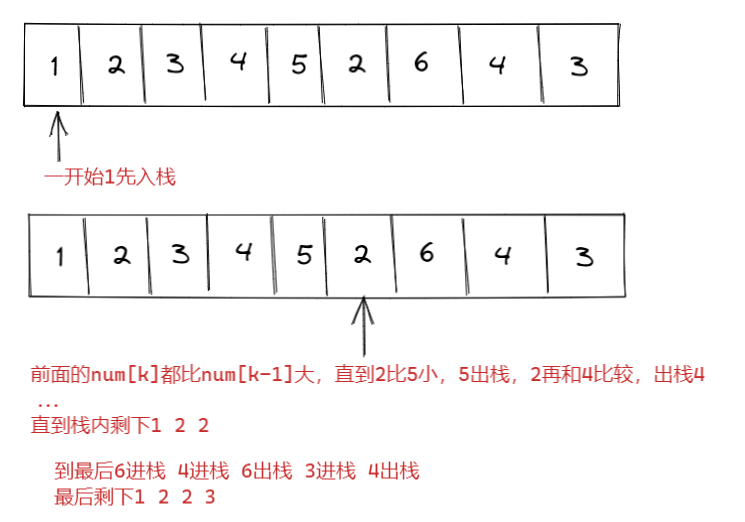
 * @param {string} num
 * @param {number} k
 * @return {string}
 */
var removeKdigits = function(num, k) {
    const stack = []
    for(let i = 0; i < num.length; i++) {
        while(k && num[i] < stack[stack.length - 1] && stack.length) {
            stack.pop()
            k--
        }
        stack.push(num[i])
    }

    // 一直进栈导致 k 还没变成 0 栈需要把最后几位出栈，凑齐删除k位  
    while(k--) {
        stack.pop()
    }

    // 去除先导零 
    while(stack.length && stack[0] === '0') {
        stack.shift()
    }
    
    const fi = stack.join('')
    return fi ? fi : '0'
};

lc316. 去除重复字母中等

题目描述

给你一个字符串 s ，请你去除字符串中重复的字母，使得每个字母只出现一次。需保证 返回结果的字典序最小（要求不能打乱其他字符的相对位置）。

示例 1：

输入：s = "bcabc"
输出："abc"

示例 2：

输入：s = "cbacdcbc"
输出："acdb"

思路

这道题的关键在于他要求的字典序最小

让我们以 bcabc为栗子

• 首先遍历到b c都是无重复的 入栈

• 然后开始遍历a， 首先a是比b c都小的

• 其次 如果要以a开头的话就得看看a后面还有没有c

  • 如果有的话 那么可以放心大胆让栈顶的元素 先出栈(之后有c)
  • 如果没有的话栈顶元素不出栈

/**
 * @param {string} s
 * @return {string}
 */
var removeDuplicateLetters = function(s) {
    const stack = []
    for(let i = 0; i < s.length; i++) {
        if(stack.indexOf(s[i]) > -1) continue

        while(stack.length && stack[stack.length - 1] > s[i] && s.indexOf(stack[stack.length - 1], i) > i) {
            stack.pop()
        }
        stack.push(s[i])
    }
    return stack.join('')
};

lc84. 柱状图中最大的矩形中等

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

输入： heights = [2,4]
输出： 4

思路

我们使用一个单调递增栈，栈中存的是「柱子的索引」。

我们希望以每根柱子 heights[i] 为 矩形的最短边，向左和向右扩展，找到它能延展到的最大宽度，计算面积 height × width。

为此我们需要知道：

• 当前柱子左边第一个比它矮的柱子索引 left[i]
• 当前柱子右边第一个比它矮的柱子索引 right[i]

最大面积是：( right[i] - left[i] - 1 ) * heights[i]

var largestRectangleArea = function(heights) {
  heights.push(0); // 添加一个哨兵高度，保证栈清空
  const stack = [-1]; // 栈中存索引，栈底放 -1 方便计算宽度
  let maxArea = 0;

  for (let i = 0; i < heights.length; i++) {
    // 如果当前柱子更矮，栈顶出栈，并计算这个栈顶柱子形成的矩形面积。
    while (stack.length > 1 && heights[i] < heights[stack[stack.length - 1]]) {
      const height = heights[stack.pop()];
      const width = i - stack[stack.length - 1] - 1;
      maxArea = Math.max(maxArea, height * width);
    }
    // 如果当前柱子更高，压栈（可能是未来右边界的左柱子）。    
    stack.push(i);
  }

  return maxArea;
};

时间复杂度：O(n) 每个柱子最多入栈和出栈各一次。

空间复杂度：O(n) 最坏情况下，栈中存储所有柱子的索引。