二叉树的遍历

lc144. 二叉树的前序遍历简单 hot

题目描述

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

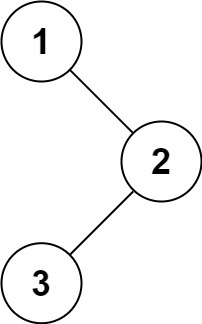
输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

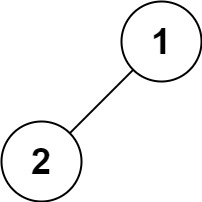
输入：root = [1,2]
输出：[1,2]

示例 5：

输入：root = [1,null,2]
输出：[1,2]

法一： 递归

思路很简单就是先递归遍历左子树再遍历右子树

时间复杂度O(n)

空间复杂度O(n)

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
 
var preorderTraversal = function(root) {
  let result = []
  const childNode = (node) => {
    if(node) {
      result.push(node.val)
        childNode(node.left)
        childNode(node.right)
      // 同样的，中序遍历则是先left 再push 再right 
      // 后序遍历则是 先left 后right 再push
      }
    }
  childNode(root)
  return result
};

法二：迭代

用栈来模拟递归

• 维护一个栈数组和一个结果数组

• 首先根节点入栈

• 由于栈是后进先出

• 首先根节点出栈，将根节点的值放在结果数组中

• 如果该根节点存在右节点，让右节点入栈

• 接着如果该根节点存在左节点，左节点入栈

var preorderTraversal = function(root) {
    const stack = []
    const list = []
    if(root) stack.push(root)
    while(stack.length > 0) {
        const curNode = stack.pop()
        list.push(curNode.val)
        if(curNode.right) stack.push(curNode.right)
        if(curNode.left) stack.push(curNode.left)
    }
    return list
};
// 中序遍历
var inorderTraversal = function(root) {
  	const stack = []
    const list = []
    while(stack.length || root) {
        while(root) {
            stack.push(root)
            root = root.left
        }
        root = stack.pop()
        list.push(root.val)
        root = root.right
    }
    return list
}

// 后序遍历
var postorderTraversal = function(root) {
  if(!root) return []
  const res = []
  const stack = []
  stack.push(root)
  while(stack.length) {
    let node = stack.pop()
    res.unshift(node.val)
    if(node.left) stack.push(node.left)
    if(node.right) stack.push(node.right)
  }
  return res
}

// 或者模仿一下先序遍历的递归
// 先序遍历是一个栈 root 进，然后右，然后左，然后出栈 [根，左，右]
// 后序遍历要得到[左，右，根]，那么就得到[根，右，左]，再翻转
var postorderTraversal = function(root) {
    const stack = []
    const list = []
    if(root) stack.push(root)
    while(stack.length > 0) {
        const curNode = stack.pop();
        list.push(curNode.val);
        if(curNode.left) stack.push(curNode.left);
        if(curNode.right) stack.push(curNode.right);
    }
    return list;
};

时间复杂度O(n)

空间复杂度O(n)

lc589. N叉树的前序遍历简单

题目描述

给定一个 N 叉树，返回其节点值的 前序遍历 。

N 叉树 在输入中按层序遍历进行序列化表示，每组子节点由空值 null 分隔（请参见示例）。

进阶：

递归法很简单，你可以使用迭代法完成此题吗?

示例 1：

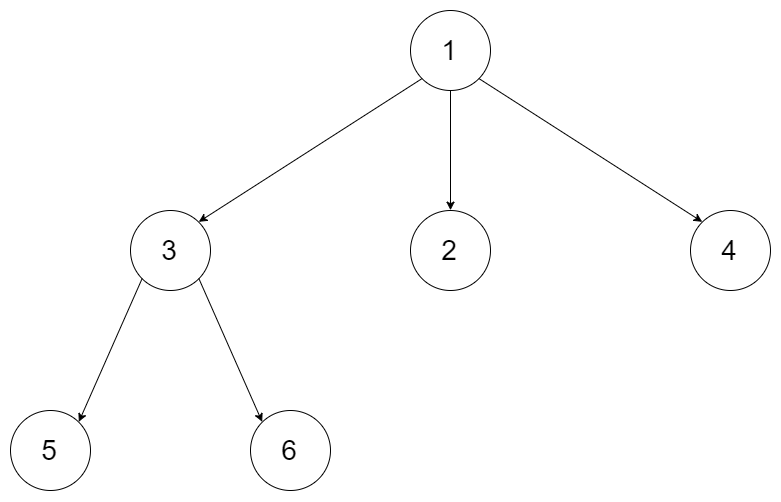
输入：root = [1,null,3,2,4,null,5,6]

输出：[1,3,5,6,2,4]

示例 2：

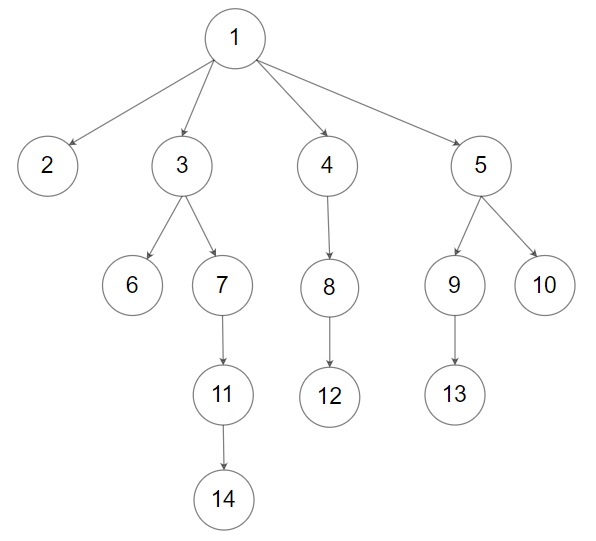
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]

输出：[1,2,3,6,7,11,14,4,8,12,5,9,13,10]

// 递归
/**
 * @param {Node|null} root
 * @return {number[]}
 */
var preorder = function(root) {
  const res = []
  const childNode = node => {
    if(node) {
      res.push(node.val)
      node.children.forEach(item => {
        childNode(item)
      })
    }
  }
  childNode(root)
  return res
};

// 迭代
var preorder = function(root) {
 	const stack = []
  const res = []
  if(root) stack.push(root)
  while(stack.length) {
    let node = stack.pop()
    res.push(node.val)
    if(node.children) {
      for(let i = node.children.length - 1; i >= 0; i--) {
        stack.push(node.children[i])
      }
    }
  }
  return res
};
// N叉🌲后序遍历
var postorderTraversal = function(root) {
  if(!root) return []
  const res = []
  const stack = []
  stack.push(root)
  while(stack.length) {
    let node = stack.pop()
    res.unshift(node.val)
    if(node.children) {
      stack.push(...node.children)
    }
  }
  return res
};

lc102. 二叉树的层序遍历中等hot

题目描述

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

示例：

二叉树：[3,9,20,null,null,15,7],
    3
   / \
  9  20
    /  \
   15   7

返回其层序遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

法一：BFS广度优先

思路：

• 每向下一层，然后把他们的值存起来
• 利用了多个数组

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function levelOrder(root: TreeNode | null): number[][] {
    if(!root) return [];
    const queue = [root];
    const res = [];
    let depth = 0;
    while (queue.length) {
        res[depth] = res[depth] || []
      // 这个queue保存了当前深度的所有节点
        const size = queue.length;
      // 把当前深度的节点的左右节点推进queue中，那就是下一个深度的所有节点
        for(let i = 0; i < size; i++) {
            const node = queue.shift();
            res[depth].push(node.val);
						
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
        depth++;
    }
    return res;
};

时间复杂度O(n)

空间复杂度O(n)

法二：DFS深度优先

• 根据树依次向下遍历，并记录每次的depth
• 然后把相应的node.val存到结果数组里面去

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    let res = []
    const dep = function(node, depth) {
        if(!node) return
        res[depth] = res[depth] || []
        res[depth].push(node.val)
        dep(node.left, depth + 1)
        dep(node.right, depth + 1)
    }
    dep(root, 0)
    return res
};

时间复杂度O(n)

空间复杂度O(h) h为树的高度

lc103. 二叉树的锯齿形层序遍历中等hot

题目描述

给定一个二叉树，返回其节点值的锯齿形层序遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

例如：

给定二叉树 [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回锯齿形层序遍历如下：

[
  [3],
  [20,9],
  [15,7]
]

思路

就是从零开始，奇数就从右往左，偶数就从左往右

/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var zigzagLevelOrder = function(root) {
    const res = []
    
    function dfs(node, depth){
        if(!node) return 

        if(!Array.isArray(res[depth])){
            res[depth] = []
        }
        // 奇数
        if(depth & 1){
            res[depth].unshift(node.val)
        }else{
            res[depth].push(node.val)
        }
        dfs(node.left, depth + 1)
        dfs(node.right, depth + 1)
    }

    dfs(root, 0)
    return res
};

时间复杂度O(n)

空间复杂度O(n)

lc958. 二叉树的完全性检验中等hot

题目描述

给定一个二叉树，确定它是否是一个完全二叉树。

百度百科中对完全二叉树的定义如下：

若设二叉树的深度为 h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。（注：第 h 层可能包含 1~ 2h 个节点。）

示例 1：

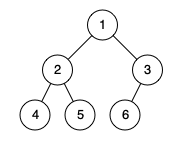
输入：[1,2,3,4,5,6]

输出：true

解释：最后一层前的每一层都是满的（即，结点值为 {1} 和 {2,3} 的两层），且最后一层中的所有结点（{4,5,6}）都尽可能地向左。

示例 2：

输入：[1,2,3,4,5,null,7]

输出：false

解释：值为 7 的结点没有尽可能靠向左侧。

思路

使用队列层序遍历。

遇到非空节点就继续将其左右孩子加入队列。

遇到空节点后，设一个标记 end = true。

如果后续还遇到非空节点，则返回 false。

var isCompleteTree = function(root) {
    let queue = [root];
    let end = false;

    while (queue.length > 0) {
        let node = queue.shift();

        if (!node) {
            end = true;
        } else {
            if (end) return false;
            queue.push(node.left);
            queue.push(node.right);
        }
    }

    return true;
};

时间复杂度O(n)

空间复杂度O(1)只用初始化一个队列 为常数个内存

lc114. 二叉树的展开为链表中等

题目描述

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。

展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

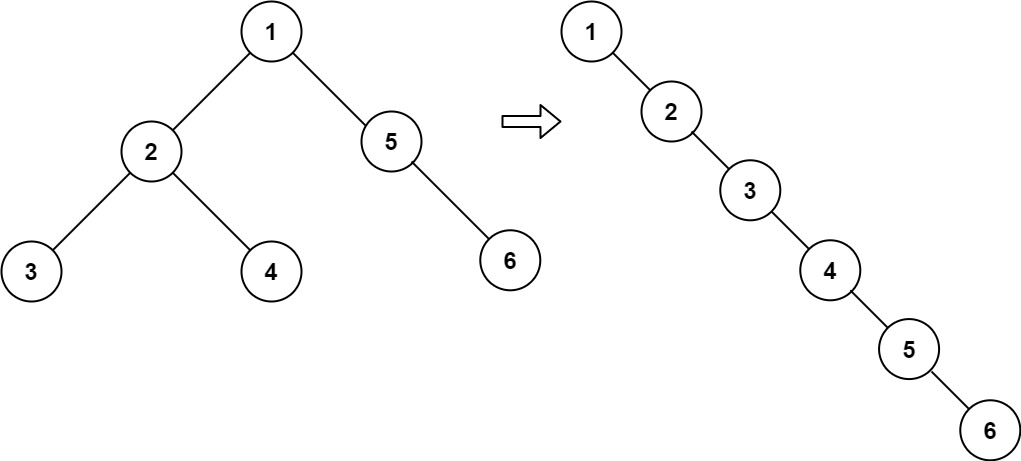
输入：root = [1,2,5,3,4,null,6]

输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []

输出：[]

示例 3：

输入：root = [0]

输出：[0]

var flatten = function(root) {
  const res = []
  const childNode = node => {
    if(node) {
      res.push(node)
      childNode(node.left)
      childNode(node.right)
    }
  }

  childNode(root)
  for(let i = 0; i < res.length - 1; i++) {
    res[i].left = null
    res[i].right = res[i + 1]
  }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。前序遍历的时间复杂度是 O(n)，前序遍历之后，需要对每个节点更新左右子节点的信息，时间复杂度也是 O(n)。
• 空间复杂度：O(n)，其中 n 是二叉树的节点数。空间复杂度取决于栈（递归调用栈或者迭代中显性使用的栈）和存储前序遍历结果的列表的大小，栈内的元素个数不会超过 n，前序遍历列表中的元素个数是 n。

原地操作, 栈模拟先序遍历

function flatten(root) {
  if (!root) return;

  const stack = [root];
  let prev = null;

  while (stack.length) {
    const node = stack.pop();

    if (prev) {
      prev.right = node;
      prev.left = null;
    }

    // 先右后左入栈，保证先序遍历顺序
    if (node.right) stack.push(node.right);
    if (node.left) stack.push(node.left);

    prev = node;
  }
}

129. 求根节点到叶节点数字之和中等hot

题目描述

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

• 例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

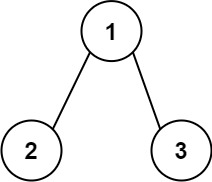
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

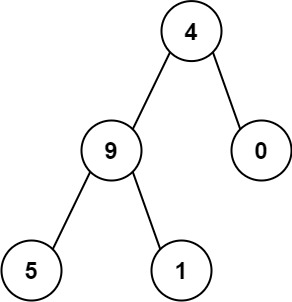
输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

思路1: 递归

我们从根节点出发，每向下一层，就将当前路径值更新为 当前值 * 10 + 当前节点的值，直到叶子节点为止，将该值加入总和。

var sumNumbers = function(root) {
    const dfs = (node, currSum) => {
        if (!node) return 0;

        let sum = currSum * 10 + node.val;

        // 如果是叶子节点
        if (!node.left && !node.right) {
            return sum;
        }

        return dfs(node.left, sum) + dfs(node.right, sum);
    };

    return dfs(root, 0);
};

时间复杂度:O(n)

空间复杂度:O(h)

bfs：层序遍历

我们在队列中同时存储：

• 当前节点 node
• 从根到当前节点构成的数字 num

当我们遇到叶子节点时，把这个 num 加入结果即可。

var sumNumbers = function(root) {
    if (!root) return 0;

    let sum = 0;
    let queue = [[root, root.val]];

    while (queue.length > 0) {
        let [node, currNum] = queue.shift();

        // 如果是叶子节点，加到总和里
        if (!node.left && !node.right) {
            sum += currNum;
        }

        // 加入左右子节点，并更新路径数值
        if (node.left) {
            queue.push([node.left, currNum * 10 + node.left.val]);
        }
        if (node.right) {
            queue.push([node.right, currNum * 10 + node.right.val]);
        }
    }

    return sum;
};

时间复杂度:O(n)

空间复杂度:O(n)

lc208. 实现 Trie (前缀树)中等hot

题目描述

Trie (opens new window)（发音类似 "try"）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

• Trie() 初始化前缀树对象。
• void insert(String word) 向前缀树中插入字符串 word 。
• boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
• boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：

输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // 返回 True
trie.search("app");     // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app");     // 返回 True

思路

对插入进行讲解一下

insert之后是这样，最里面有一个end属性，searchPrefix也是一层一层的找

class TrieNode {
  children: Map<string, TrieNode>;
  isEnd: boolean;

  constructor() {
    this.children = new Map();
    this.isEnd = false;
  }
}

class Trie {
  root: TrieNode;

  constructor() {
    this.root = new TrieNode();
  }

  insert(word: string): void {
    let node = this.root;
    for (const ch of word) {
      if (!node.children.has(ch)) {
        node.children.set(ch, new TrieNode());
      }
      node = node.children.get(ch)!;
    }
    node.isEnd = true;
  }

  search(word: string): boolean {
    let node = this.root;
    for (const ch of word) {
      if (!node.children.has(ch)) return false;
      node = node.children.get(ch)!;
    }
    return node.isEnd;
  }

  startsWith(prefix: string): boolean {
    let node = this.root;
    for (const ch of prefix) {
      if (!node.children.has(ch)) return false;
      node = node.children.get(ch)!;
    }
    return true;
  }
}