小宋爱睡觉
  • 排序
Crucials
2021-11-30

十大排序

# 冒泡排序

冒泡排序动画

思路

  • 从头开始比较两个相邻的数

  • 前者大于后者就交换

  • 每一轮最后的数最大

const bubbleSort = function (arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        let temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
      }
    }
  }
  return arr;
};

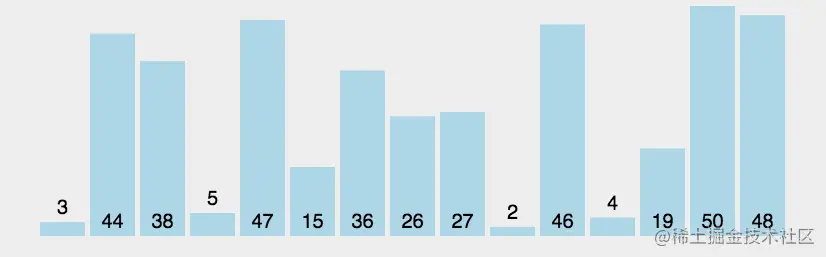
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

console.log(bubbleSort(arr));
// [2,  3,  4,  5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

时间复杂度O(n²)

空间复杂度O(1)

第一次改进

提前退出

function bubbleSort1(arr) {
  for (let i = 0; i < arr.length; i++) {
    // 提前退出冒泡循环的标识位
    let flag = false;
    for (let j = 0; j < arr.length - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        const temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        flag = true;
        // 表示发生了数据交换
      }
    }
    // 没有数据交换
    if (!flag) break;
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

冒泡排序总会执行(N-1)+(N-2)+(N-3)+..+2+1趟，但如果运行到当中某一趟时排序已经完成，或者输入的是一个有序数组，那么后边的比较就都是多余的，为了避免这种情况，我们增加一个flag，判断排序是否在中途就已经完成（也就是判断有无发生元素交换）

记录每次最后进行交换的位置，避免每次都得从头开始

const bubbleSort = function (arr) {
  let i = arr.length - 1; //初始时,最后位置保持不变
  while (i > 0) {
    let pos = 0; //每趟开始时,无记录交换
    for (var j = 0; j < i; j++)
      if (arr[j] > arr[j + 1]) {
        pos = j; //记录交换的位置
        var tmp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = tmp;
      }
    i = pos; //为下一趟排序作准备
  }
  return arr;
};

const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

console.log(bubbleSort(arr));
// [2,  3,  4,  5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

第二次改进

正向和反向冒泡，记录最大和最小值

const bubbleSort = function (arr) {
  let low = 0;
  let high = arr.length - 1;
  while (low < high) {
    for (let i = low; i < high; i++) {
      if (arr[i] > arr[i + 1]) {
        let tmp = arr[i];
        arr[i] = arr[i + 1];
        arr[i + 1] = tmp;
      }
    }
    --high;

    for (let j = high; j > low; j--) {
      if (arr[j] > arr[j + 1]) {
        let tmp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = tmp;
      }
    }
  }
  ++low;

  return arr;
};

const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

console.log(bubbleSort(arr));
// [2,  3,  4,  5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

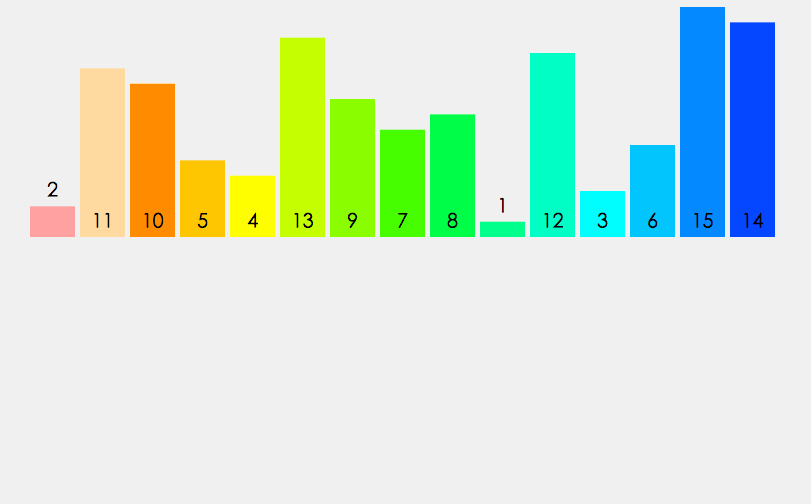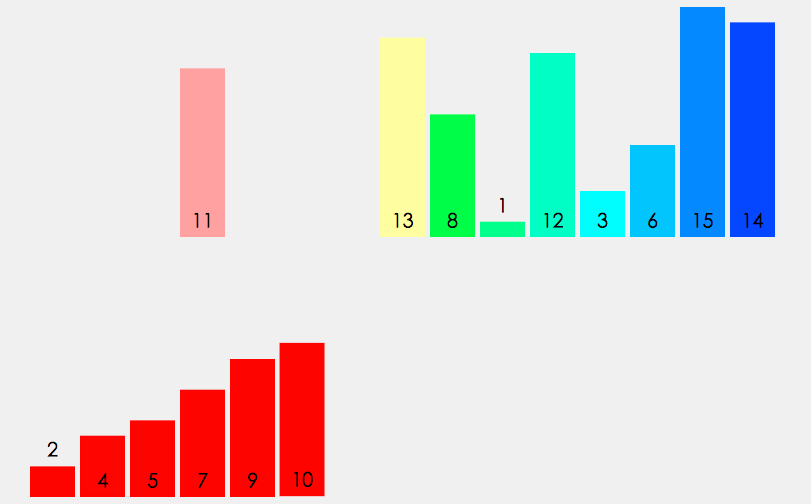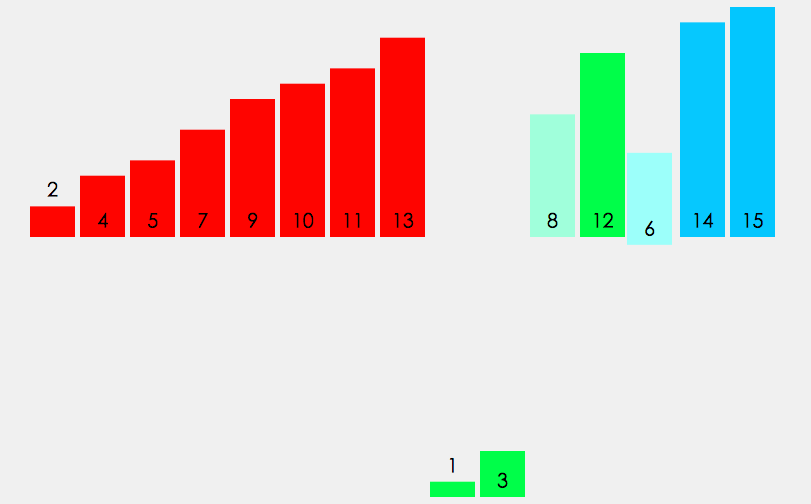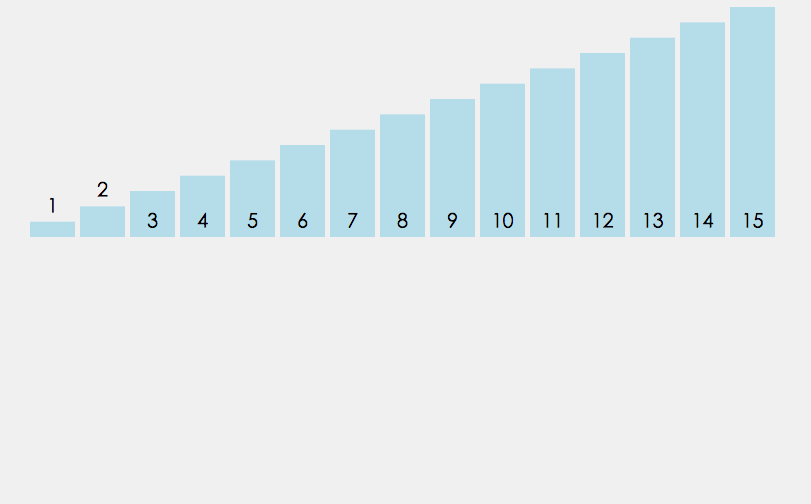
# 快速排序

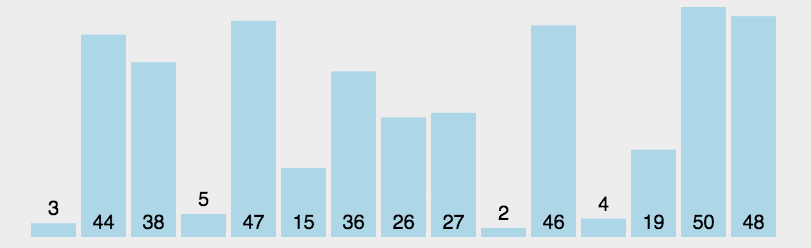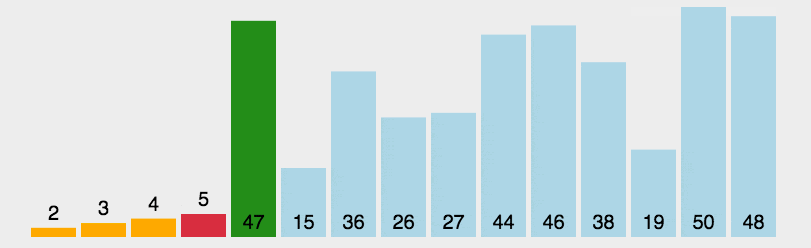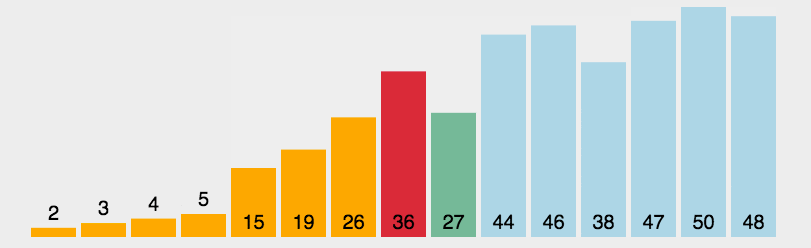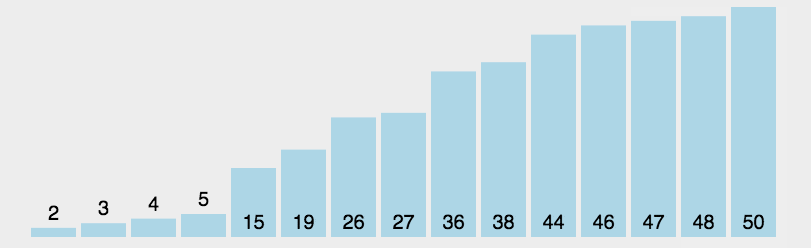
  • 先找到一个基准点（一般指数组的中部），然后数组被该基准点分为两部分，依次与该基准点数据比较，如果比它小，放左边；反之，放右边。
  • 左右分别用一个空数组去存储比较后的数据。
  • 最后递归执行上述操作，直到数组长度 <= 1

先写一下用两个数组的

固定基准值

const sort = arr => {
		
	  if (arr.length < 2) return arr;
	  
	  // 固定基准值
	  let pivot = arr[0];

	  let left = [];
	  let right = [];
		
	  // 从1开始
	  for (let i = 1, total = arr.length; i < total; i++) {
	    if (arr[i] < pivot) left.push(arr[i]);
	    else right.push(arr[i]);
	  };
	  
	  return [
	    ...sort(left),
	    pivot,
	    ...sort(right)
	  ];
	};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

基准值去三数之中

	const sort = arr => {
		
	  if (arr.length < 2) return arr;
	  
	  // 使用三数取中
	  let start = arr[0];
	  let middle = arr[Math.floor(arr.length/2)];
	  let end = arr[arr.length-1];
	  let pivot = middle;
	  
		if (start > middle && start < end) {
			pivot = start;
			arr.splice(0, 1)
		} else if (end > middle && end < start) {
			pivot = end;
			arr.splice(arr.length - 1, 1)
		} else if (pivot === middle) {
			arr.splice(Math.floor(arr.length / 2), 1)
		}

	  let left = [];
	  let right = [];
	
	  for (let i = 0, total = arr.length; i < total; i++) {
	    if (arr[i] < pivot) left.push(arr[i]);
	    else right.push(arr[i]);
	  };
	  
	  return [
	    ...sort(left),
	    pivot,
	    ...sort(right)
	  ];
	};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

当数据少于一定程度的时候用插入排序法

function insertArr(arr){
		for(let i = 1 , len = arr.length; i < len ; i++){
			let preIndex = i - 1;
			let current = arr[i];
			while(preIndex >= 0 && current < arr[preIndex] ){
				arr[preIndex+1] = arr[preIndex]
				preIndex--;
			}
			arr[preIndex+1] = current;
		}
		return arr;
	}
			
	const sort = arr => {

		if (arr.length < 2) return arr;

		// 当数组长度小于10用插入排序
		if (arr.length < 10) {
			return insertArr(arr);
		}

		// 使用三数取中
		let start = arr[0];
		let middle = arr[Math.floor(arr.length / 2)];
		let end = arr[arr.length - 1];
		let pivot = middle;

		if (start > middle && start < end) {
			pivot = start;
			arr.splice(0, 1)
		} else if (end > middle && end < start) {
			pivot = end;
			arr.splice(arr.length - 1, 1)
		} else if (pivot === middle) {
			arr.splice(Math.floor(arr.length / 2), 1)
		}

		let left = [];
		let right = [];


		for (let i = 0, total = arr.length; i < total; i++) {
			if (arr[i] < pivot) {
				left.push(arr[i]);
			} else {
				right.push(arr[i]);
			}
		};

		return [
			...sort(left),
			pivot,
			...sort(right)
		];
	};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

把相同元素也聚集到一个数组中

function getMiddle(a, b, c) {
		var min = Math.min(a, b, c);
		var max = Math.max(a, b, c);
		var middle = a + b + c - min - max;
		return middle;
	}
	
	function insertArr(arr){
		for(let i = 1 , len = arr.length; i < len ; i++){
			let preIndex = i - 1;
			let current = arr[i];
			while(preIndex >= 0 && current < arr[preIndex] ){
				arr[preIndex+1] = arr[preIndex]
				preIndex--;
			}
			arr[preIndex+1] = current;
		}
		return arr;
	}
			
	const sort = arr => {

		if (arr.length < 2) return arr;

		// 当数组长度小于10用插入排序
		if (arr.length < 10) {
			return insertArr(arr);
		}

		// 使用三数取中
		let start = arr[0];
		let middle = arr[Math.floor(arr.length / 2)];
		let end = arr[arr.length - 1];
		let pivot = getMiddle(start, middle, end);
		
		let left = [];
		let right = [];
		let alike = [];

		for (let i = 0, total = arr.length; i < total; i++) {
			if (arr[i] < pivot) {
				left.push(arr[i]);
			} else if (arr[i] > pivot) {
				right.push(arr[i]);
			} else {
				alike.push(arr[i])
			}
		};

		return [
			...sort(left),
			...alike,
			...sort(right)
		];
	};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

接下来的是空间复杂度为O(1)的写法

function quickSort(nums) {
  // 递归排序基数左右两边的序列
  function recursive(arr, left, right) {
    if(left >= right)  return;
    let index = partition(arr, left, right);
    recursive(arr, left, index - 1);
    recursive(arr, index + 1, right);
    return arr;
  }
  // 将小于基数的数放到基数左边，大于基数的数放到基数右边，并返回基数的位置
  function partition(arr, left, right) {
    // 取第一个数为基数
    let temp = arr[left];
    while(left < right) {
      while(left < right && arr[right] >= temp)  right--;
      arr[left] = arr[right];
      while(left < right && arr[left] < temp)  left++;
      arr[right] = arr[left];
    }
    // 修改基数的位置
    arr[left] = temp;
    return left;
  }
  recursive(nums, 0, nums.length-1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

时间复杂度都是O(nlogn) 最差情况是一个有序的数据，然后基准值为最后一个数，退化为O(n^2)

# 选择排序

思路

selection-sort.gif

  • 进入第一次循环 记录当前循环索引i
  • 对 i + 1到数组最后 进入第二次循环 找出最小的数 与 i 替换
const selectionSort = function (arr) {
  let minIndex;
  for (let i = 0; i < arr.length - 1; i++) {
    minIndex = i;

    for (let j = i + 1; j < arr.length; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j;
      }
    }

    let temp = arr[minIndex];
    arr[minIndex] = arr[i];
    arr[i] = temp;
  }
  return arr;
};

const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

console.log(selectionSort(arr));
// [2,  3,  4,  5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]


// 或者
function selectSort(nums) {
  for (let i = 0; i < nums.length - 1; i++) {
    for (let j = i; j < nums.length; j++) {
      if (nums[j] < nums[i]) {
        [nums[i], nums[j]] = [nums[j], nums[i]];
      }
    }
  }
  return nums;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

时间复杂度O(n²)

空间复杂度O(1)

# 插入排序

思路

insertion-sort.gif

  • 排序开始 默认第一个数是有序的

  • 后面每加入一个数字 都和前一位的比较

    • 如果大 就直接插入在后面
    • 如果小 则继续向前
const insertSort = function (arr) {
  for (let i = 1; i < arr.length; i++) {
    let cur = arr[i];
    let j = i - 1;
    while (j >= 0 && arr[j] > cur) {
      arr[j + 1] = arr[j];
      j--;
    }

    arr[j + 1] = cur;
  }
  return arr;
};

// 或者
function insertSort(nums) {
  for (let i = 0; i < nums.length; i++) {
    for (let j = i; j >= 0; j--) {
      if (nums[j] < nums[j - 1]) {
        [nums[j], nums[j - 1]] = [nums[j - 1], nums[j]];
      } else {
        break;
      }
    }
  }
  return nums;
}
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

console.log(insertSort(arr));
// [2,  3,  4,  5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

时间复杂度O(n^2)

空间复杂度O(1)

是稳定的排序算法

改进 加入二分

const insertSort = function (arr) {
  for (let i = 1; i < arr.length; i++) {
    let cur = arr[i];

    let left = 0,
      right = arr.length - 1;
    let middle = +((left + right) / 2);

    if (cur < arr[middle]) {
      right = --middle;
    } else {
      left = ++middle;
    }

    for (let j = i - 1; j >= left; j--) {
      arr[j + 1] = arr[j];
    }

    arr[left] = cur;
  }
  return arr;
};

const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];

console.log(insertSort(arr));
// [2,  3,  4,  5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 堆排序

思路

  1. 将待排序序列构造成一个大顶堆

    注意：这里使用的是数组，而不是一颗二叉树

  2. 此时：整个序列的 最大值就是堆顶的根节点

  3. 将其 与末尾元素进行交换，此时末尾就是最大值

  4. 然后将剩余 n-1 个元素重新构造成一个堆，这样 就会得到 n 个元素的次小值。如此反复，便能的得到一个有序序列。

先随便找一个乱序数组

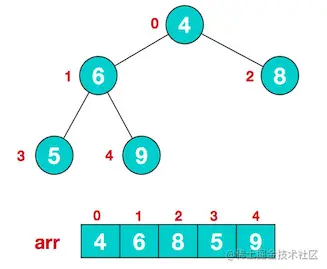
构造大顶堆

此时从最后一个非叶子节点开始调整，从左到右，从上到下进行调整。

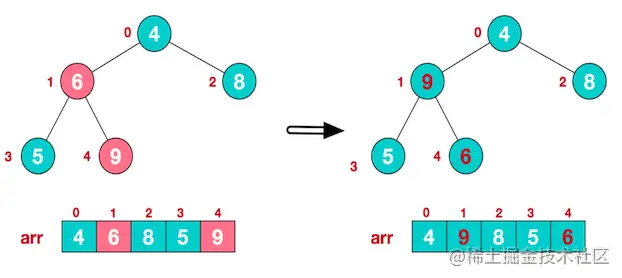
叶节点不用调整，第一个非叶子节点 arr.length/2-1 = 5/2-1 = 1，也就是 元素为 6 的节点。

比较时：先让 5 与 9 比较，得到最大的那个，再和 6 比较，发现 9 大于 6，则调整他们的位置。

img

  1. 找到第二个非叶子节点 4，由于 [4,9,8] 中，9 元素最大，则 4 和 9 进行交换

img

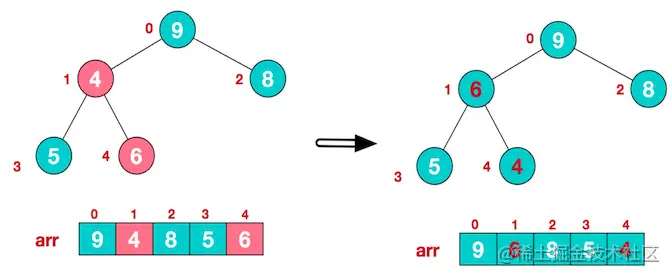
  1. 此时，交换导致了子根 [4,5,6] 结构混乱，将其继续调整。[4,5,6] 中 6 最大，将 4 与 6 进行调整。

img

此时，就将一个无序序列构造成了一个大顶堆。

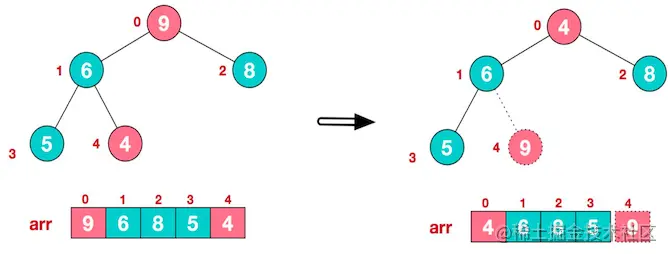
接着将堆顶元素和末尾元素进行交换

将堆顶元素与末尾元素进行交换，使其末尾元素最大。然后继续调整，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换

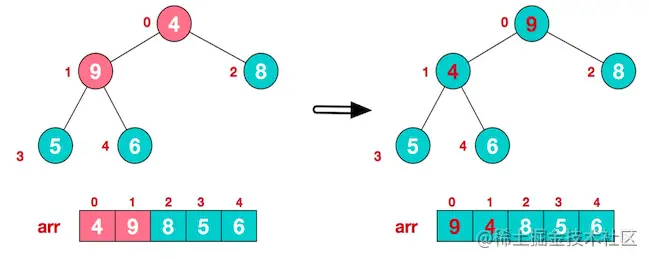
  1. 将堆顶元素 9 和末尾元素 4 进行交换

img

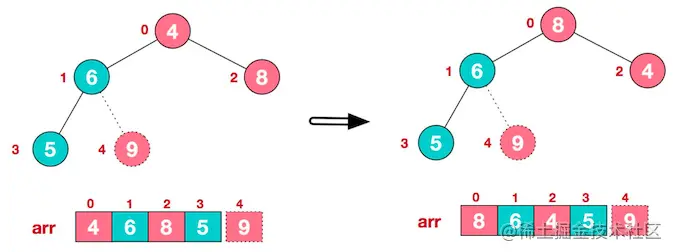
  1. 重新调整结构，使其继续满足堆定义

img

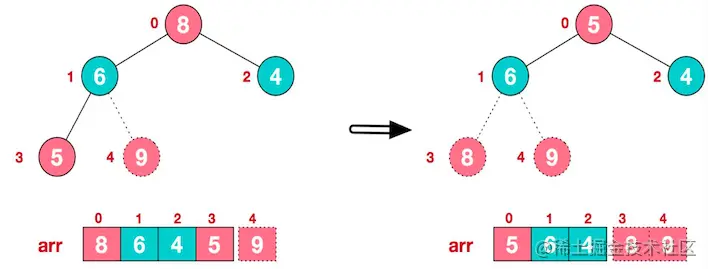
  1. 再将堆顶元素 8 与末尾元素 5 进行交换，得到第二大元素 8

img

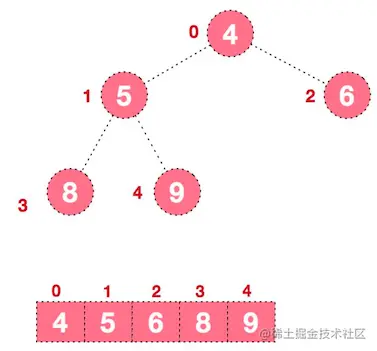
  1. 后续过程，继续进行调整、交换，如此反复进行，最终使得整个序列有序

img

  1. 第一步构建初始堆：是自底向上构建，从最后一个非叶子节点开始。
  2. 第二步就是下沉操作让尾部元素与堆顶元素交换，最大值被放在数组末尾，并且缩小数组的length，不参与后面大顶堆的调整
  3. 第三步就是调整：是从上到下，从左到右,因为堆顶元素下沉到末尾了，要重新调整这颗大顶堆
function heapSort(items) {
  let heapSize = items.length;
  // 构建好了一个大顶堆
  buildHeap(items, heapSize);
	// 进行下沉 大顶堆是最大元素下沉到末尾
  for (let i = items.length - 1; i >= 0; i--) {
    swap(items, 0, i);
    // 下沉后的元素不参与到大顶堆的调整
    --heapSize;
    // 重新调整大顶堆
    maxHeapify(items, 0, heapSize);
  }
  return items;
}
// 自下而上构建一颗大顶堆
function buildHeap(items, heapSize) {
  for (let i = Math.floor(heapSize / 2) - 1; i >= 0; i--) {
    maxHeapify(items, i, heapSize);
  }
}
// 从左向右，自上而下的调整节点
function maxHeapify(items, i, heapSize) {
  let l = 2 * i + 1;
  let r = 2 * i + 2;
  let large = i;
  if (l < heapSize && items[l] > items[large]) {
    large = l;
  }
  if (r < heapSize && items[r] > items[large]) {
    large = r;
  }
  if (large !== i) {
    swap(items, large, i);
    // 继续调整下面的非叶子节点
    maxHeapify(items, large, heapSize);
  }
}
function swap(items, i, j) {
  [items[i], items[j]] = [items[j], items[i]];
}

var items = [1, 9, 2, 8, 3, 7, 4, 6, 5];
console.log(heapSort(items));
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

最好：O(n * logn)，logn是调整最大堆所花的时间。

最坏：O(n * logn)

平均：O(n * logn)

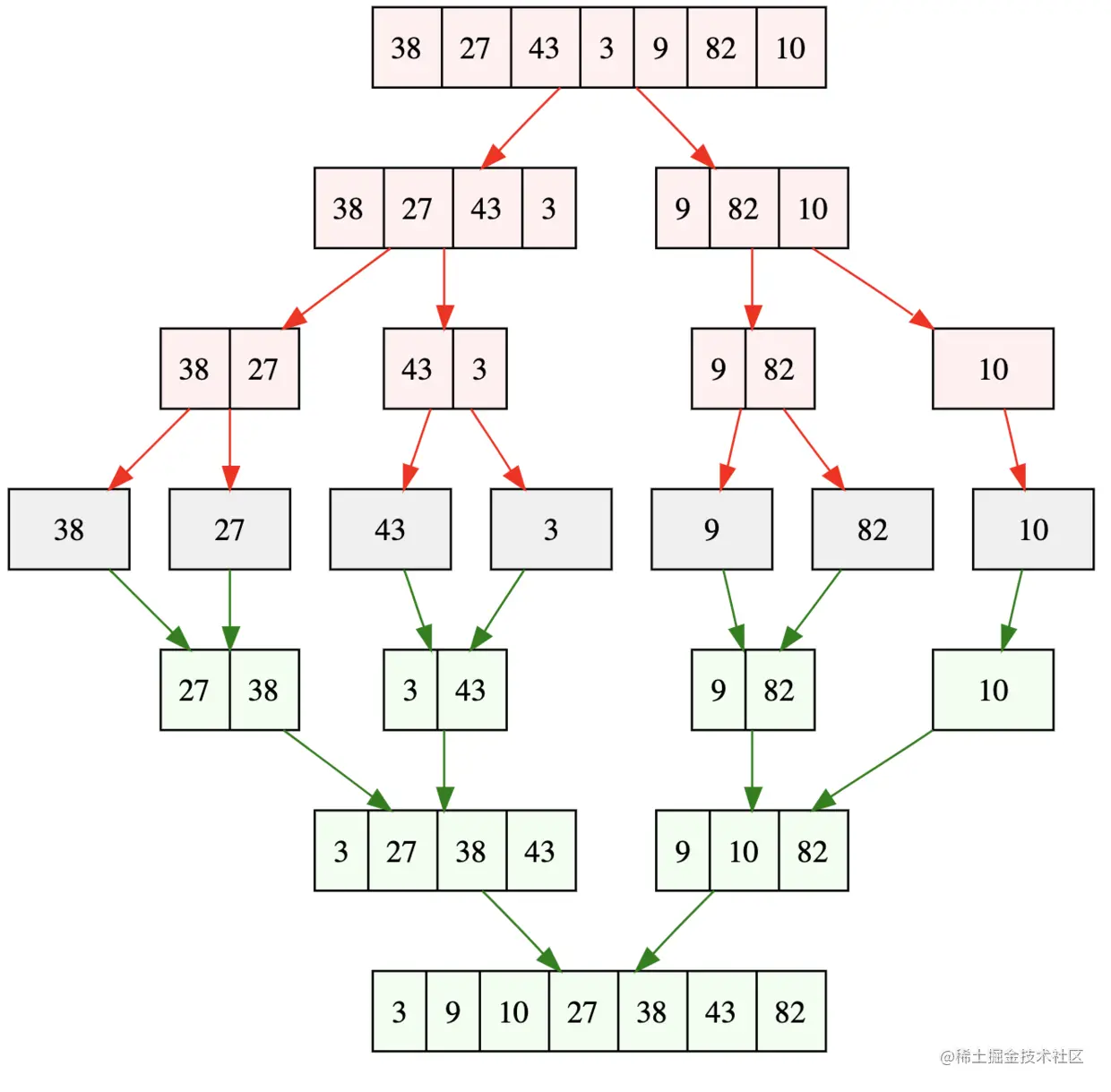
# 归并排序

merge-sort-example.png

merge-sort.gif

const mergeSort = arr => {
	//采用自上而下的递归方法
	const len = arr.length;
	if (len < 2) {
		return arr;
	}
	// length >> 1 和 Math.floor(len / 2) 等价
	let middle = Math.floor(len / 2),
		left = arr.slice(0, middle),
		right = arr.slice(middle); // 拆分为两个子数组
	return merge(mergeSort(left), mergeSort(right));
};

const merge = (left, right) => {
	const result = [];

	while (left.length && right.length) {
		// 注意: 判断的条件是小于或等于，如果只是小于，那么排序将不稳定.
		if (left[0] <= right[0]) {
			result.push(left.shift());
		} else {
			result.push(right.shift());
		}
	}

	while (left.length) result.push(left.shift());

	while (right.length) result.push(right.shift());

	return result;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

时间复杂度O(nlogn)

空间复杂度O(n)

# 希尔排序

通过某个增量 gap，将整个序列分给若干组，从后往前进行组内成员的比较和交换，随后逐步缩小增量至 1。希尔排序类似于插入排序，只是一开始向前移动的步数从 1 变成了 gap。

function shellSort(nums) {
  let len = nums.length;
  // 初始步数
  let gap = parseInt(len / 2);
  // 逐渐缩小步数
  while(gap) {
    // 从第gap个元素开始遍历
    for(let i=gap; i<len; i++) {
      // 逐步其和前面其他的组成员进行比较和交换
      for(let j=i-gap; j>=0; j-=gap) {
        if(nums[j] > nums[j+gap]) {
          [nums[j], nums[j+gap]] = [nums[j+gap], nums[j]];
        }
        else {
          break;
        }
      }
    }
    gap = parseInt(gap / 2);
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

最好：O(n * logn)，步长不断二分。 最坏：O(n * logn) 平均：O(n * logn)

# 桶排序

取 n 个桶，根据数组的最大值和最小值确认每个桶存放的数的区间，将数组元素插入到相应的桶里，最后再合并各个桶。

function bucketSort(nums) {
  // 桶的个数，只要是正数即可
  let num = 5;
  let max = Math.max(...nums);
  let min = Math.min(...nums);
  // 计算每个桶存放的数值范围，至少为1，
  let range = Math.ceil((max - min) / num) || 1;
  // 创建二维数组，第一维表示第几个桶，第二维表示该桶里存放的数
  let arr = Array.from(Array(num)).map(() => Array().fill(0));
  nums.forEach(val => {
    // 计算元素应该分布在哪个桶
    let index = parseInt((val - min) / range);
    // 防止index越界，例如当[5,1,1,2,0,0]时index会出现5
    index = index >= num ? num - 1 : index;
    let temp = arr[index];
    // 插入排序，将元素有序插入到桶中
    let j = temp.length - 1;
    while(j >= 0 && val < temp[j]) {
      temp[j+1] = temp[j];
      j--;
    }
    temp[j+1] = val;
  })
  // 修改回原数组
  let res = [].concat.apply([], arr);
  nums.forEach((val, i) => {
    nums[i] = res[i];
  })
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

最好：O(n)，每个数都在分布在一个桶里，这样就不用将数插入排序到桶里了(类似于计数排序以空间换时间)。 最坏：O(n²)，所有的数都分布在一个桶里。 平均：O(n + k)，k表示桶的个数

# 基数排序

使用十个桶 0-9，把每个数从低位到高位根据位数放到相应的桶里，以此循环最大值的位数次。但只能排列正整数，因为遇到负号和小数点无法进行比较。

function radixSort(nums) {
  // 计算位数
  function getDigits(n) {
    let sum = 0;
    while(n) {
      sum++;
      n = parseInt(n / 10);
    }
    return sum;
  }
  // 第一维表示位数即0-9，第二维表示里面存放的值
  let arr = Array.from(Array(10)).map(() => Array());
  let max = Math.max(...nums);
  let maxDigits = getDigits(max);
  for(let i=0, len=nums.length; i<len; i++) {
    // 用0把每一个数都填充成相同的位数
    nums[i] = (nums[i] + '').padStart(maxDigits, 0);
    // 先根据个位数把每一个数放到相应的桶里
    let temp = nums[i][nums[i].length-1];
    arr[temp].push(nums[i]);
  }
  // 循环判断每个位数
  for(let i=maxDigits-2; i>=0; i--) {
    // 循环每一个桶
    for(let j=0; j<=9; j++) {
      let temp = arr[j]
      let len = temp.length;
      // 根据当前的位数i把桶里的数放到相应的桶里
      while(len--) {
        let str = temp[0];
        temp.shift();
        arr[str[i]].push(str);
      }
    }
  }
  // 修改回原数组
  let res = [].concat.apply([], arr);
  nums.forEach((val, index) => {
    nums[index] = +res[index];
  }) 
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

最好：O(n * k)，k表示最大值的位数。 最坏：O(n * k) 平均：O(n * k)

# 计数排序

以数组元素值为键，出现次数为值存进一个临时数组，最后再遍历这个临时数组还原回原数组。因为 JavaScript 的数组下标是以字符串形式存储的，所以计数排序可以用来排列负数，但不可以排列小数。

function countingSort(nums) {
  let arr = [];
  let max = Math.max(...nums);
  let min = Math.min(...nums);
  // 装桶
  for(let i=0, len=nums.length; i<len; i++) {
    let temp = nums[i];
    arr[temp] = arr[temp] + 1 || 1;
  }
  let index = 0;
  // 还原原数组
  for(let i=min; i<=max; i++) {
    while(arr[i] > 0) {
      nums[index++] = i;
      arr[i]--;
    }
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

最好：O(n + k)，k是最大值和最小值的差。 最坏：O(n + k) 平均：O(n + k)

上次更新: 2022/03/10, 14:51:31
Copyright © 2021-2022 粤ICP备2021165371号