lc209. 长度最小的子数组/最短中等hot

题目描述

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度**。**如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

思路:滑动窗口 前缀和

var minSubArrayLen = function(target, nums) {
  const len = nums.length
  const sum = new Array(len + 1).fill(0)
  let l = 0, r = 0, min = +Infinity
  while(r <= len) {
    if(sum[r] - sum[l] < target) {
      sum[++r] = sum[r - 1] + nums[r - 1]
    } else {
      min = Math.min(min, r - l)
      l++
    }
  }
  // 最后一步判断 是否所有数加起来是否小于target 或者判断min是否还等于+Infinity也可以
  return sum[r - 1] < target ? 0: min
};

时间复杂度:O(n)

空间复杂度:O(n)

降低空间复杂度

var minSubArrayLen = function (target, nums) {
  const len = nums.length;
  // const sum = new Array(len + 1).fill(0)
  let l = 0,
    r = 0,
    min = +Infinity,
    sum = 0;
  while (r < len) {
    sum += nums[r];
    while (sum >= target) {
      min = Math.min(min, r - l + 1);
      sum -= nums[l];
      l++;
    }
    r++;
  }
  return min === +Infinity ? 0 : min;
};

时间复杂度:O(n)

空间复杂度:O(1)

lc239. 滑动窗口最大值困难

题目描述

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值

---------------               -----

[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

示例 2：

输入：nums = [1], k = 1
输出：[1]

示例 3：

输入：nums = [1,-1], k = 1
输出：[1,-1]

示例 4：

输入：nums = [9,11], k = 2
输出：[11]

示例 5：

输入：nums = [4,-2], k = 2
输出：[4]

法二 双向队列(单调队列)

思路：

我们使用一个双端队列（deque），队列中维护的是**“当前窗口内可能成为最大值的元素索引”**，并保持队列中：

• 队首：始终是当前窗口的最大值索引
• 队列中的索引对应的元素值是单调递减的（从队首到队尾）

步骤

1. 遍历数组的每个元素 nums[i]
2. 每次加入新元素时：
   • 移除队尾所有 小于等于 nums[i] 的元素（它们不可能成为最大值了）
   • 将当前索引 i 加入队尾
3. 检查队首元素是否已滑出窗口（i - k + 1 > deque[0]），如果是就从队首移除
4. 从第 k - 1 项开始，每次将 nums[deque[0]] 加入结果数组

function maxSlidingWindow(nums, k) {
  const deque = [];  // 存放索引
  const result = [];

  for (let i = 0; i < nums.length; i++) {
    // 移除队尾所有比当前元素小的索引
    while (deque.length > 0 && nums[i] >= nums[deque[deque.length - 1]]) {
      deque.pop();
    }

    deque.push(i); // 加入当前索引

    // 每次窗口滑动之后，移除滑出窗口的索引
    if (deque[0] <= i - k) {
      deque.shift();
    }

    // 只有窗口形成了，才加入结果
    if (i >= k - 1) {
      result.push(nums[deque[0]]);
    }
  }
  return result;
}

时间复杂度：O(n)，每个元素最多被插入和移除一次

空间复杂度：O(k)，队列最多存储 k 个索引

lc03. 无重复字符的最长子串中等hot

题目描述：

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

示例 4:

输入: s = ""
输出: 0

我们使用一个滑动窗口 [left, right] 来表示当前不含重复字符的子串：

1. 用一个 Set 来记录当前窗口中的字符；
2. 如果 right 指向的字符不在 Set 中，就加入窗口并更新最大长度；
3. 如果 right 指向的字符已经在 Set 中（说明重复了），我们就不断从 left 开始移除字符，直到没有重复为止；
4. 整个过程保证了每个字符最多进出窗口一次，时间复杂度为 O(n)。

function lengthOfLongestSubstring(s: string): number {
  const seen = new Set();
  let left = 0;
  let max = 0;

  for(let right = 0; right < s.length; right++) {
    while (seen.has(s[right])) {
        seen.delete(s[left]);
        left++;
    }

    seen.add(s[right]);
    max = Math.max(max, right - left + 1);
  }

  return max;
};

时间复杂度O(n) 每个字符最多访问两次（一次加入，一次移出）；

空间复杂度O(k)k 是字符集大小（英文字母最多 26~128 个）。

lc76. 最小覆盖子串困难hot

题目描述

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

• 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
• 如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"

示例 2：

输入：s = "a", t = "a"
输出："a"

示例 3:

输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

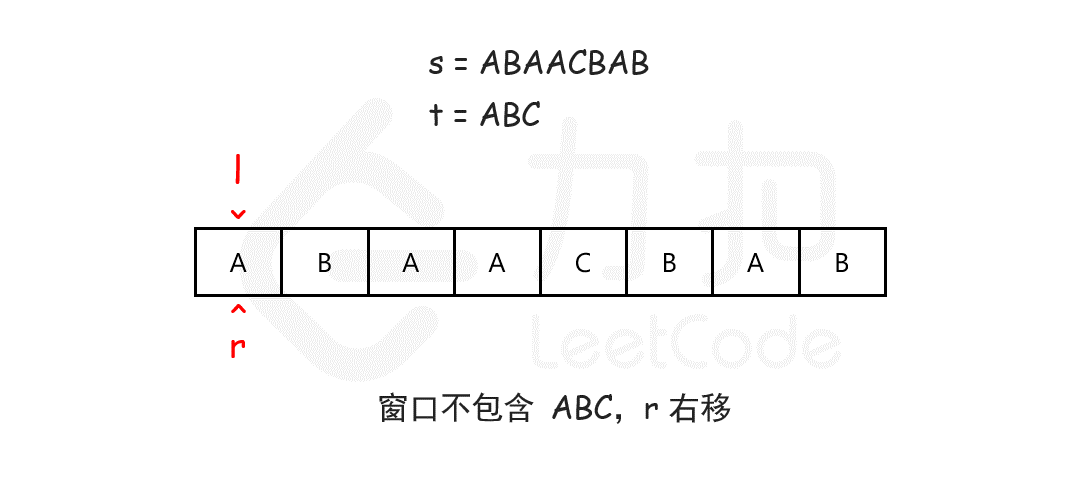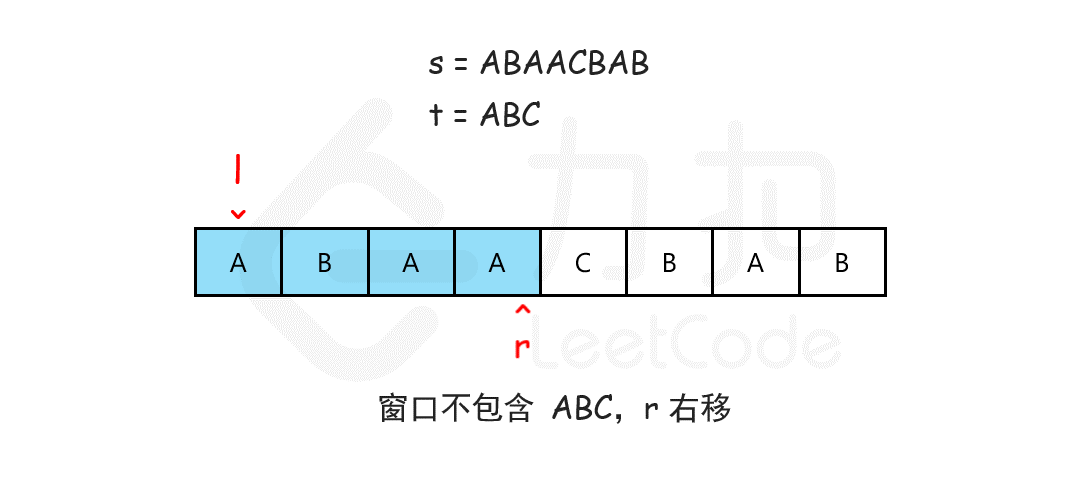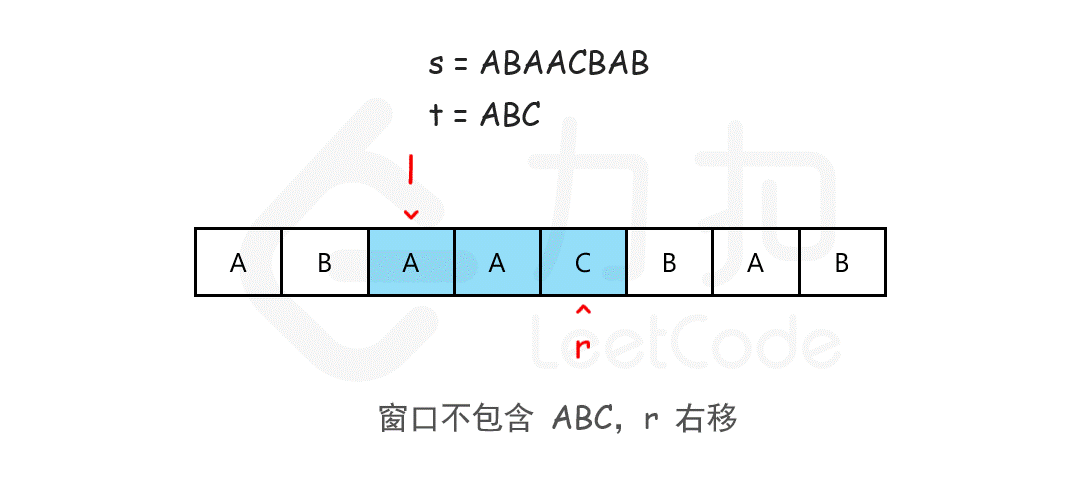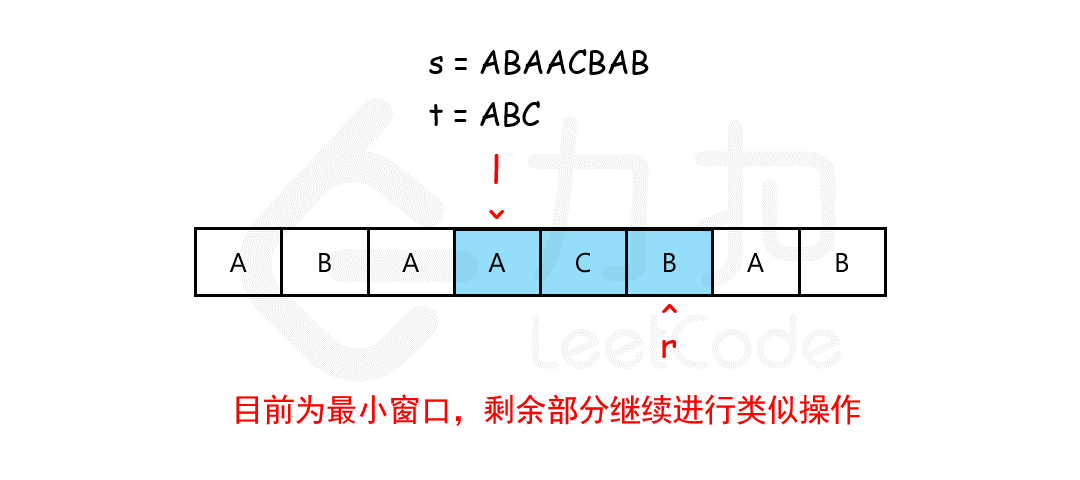
思路

• 用一个哈希表 need 记录 t 中每个字符需要的个数。
• 用一个哈希表 window 记录当前窗口中每个字符出现的个数。
• 用双指针维护一个滑动窗口 [left, right)，初始都在 0。
• 向右移动 right 扩大窗口，直到包含所有 t 中的字符。
• 然后移动 left 收缩窗口，尽可能缩小。
• 每次窗口有效（即包含所有 t 中字符）时，记录最小窗口长度与位置。
• 最后返回这个最小窗口子串。

function minWindow(s, t) {
  if (s.length === 0 || t.length === 0) return "";

  // 1. 统计 t 中每个字符的出现次数
  const need = new Map();
  for (const char of t) {
    need.set(char, (need.get(char) || 0) + 1);
  }

  // 2. 初始化滑动窗口
  const window = new Map();
  let left = 0, right = 0; // 窗口左右边界
  let valid = 0; // 满足 need 条件的字符种类数
  let start = 0, minLen = Infinity; // 最小窗口的起点和长度

  // 3. 扩展窗口
  while (right < s.length) {
    const c = s[right];
    right++; // 扩大窗口右边界

    // 更新窗口内数据
    if (need.has(c)) {
      window.set(c, (window.get(c) || 0) + 1);
      if (window.get(c) === need.get(c)) {
        valid++; // 当前字符已满足所需数量
      }
    }

    // 4. 尝试收缩窗口
    while (valid === need.size) {
      // 当前窗口包含 t 中所有字符
      if (right - left < minLen) {
        start = left;
        minLen = right - left;
      }

      const d = s[left];
      left++; // 缩小左边界

      if (need.has(d)) {
        if (window.get(d) === need.get(d)) {
          valid--; // 收缩后不再满足条件
        }
        window.set(d, window.get(d) - 1);
      }
    }
  }

  return minLen === Infinity ? "" : s.slice(start, start + minLen);
}

时间复杂度:O(s + t)

空间复杂度:O(s + t)

lc438. 找到字符串中所有字母异位词中等hot

题目描述

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

示例 1:

输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。

示例 2:

输入: s = "abab", p = "ab"
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。

核心步骤：

1. 用两个长度为 26 的数组（表示 a-z）来统计字母频率：
   • pCount：记录字符串 p 的字符频率；
   • sCount：记录当前窗口中字符的频率。
2. 使用固定长度的滑动窗口：
   • 窗口大小为 p.length；
   • 每次移动窗口，比较 sCount 和 pCount 是否一致；
3. 一致就说明是一个异位词，记录当前窗口的起始索引。

function findAnagrams(s, p) {
  const res = [];
  const sLen = s.length, pLen = p.length;

  if (sLen < pLen) return res;

  const sCount = new Array(26).fill(0);
  const pCount = new Array(26).fill(0);

  // 初始化频率数组
  for (let i = 0; i < pLen; i++) {
    sCount[s.charCodeAt(i) - 97]++;
    pCount[p.charCodeAt(i) - 97]++;
  }

  if (arraysEqual(sCount, pCount)) res.push(0);

  // 滑动窗口
  for (let i = pLen; i < sLen; i++) {
    sCount[s.charCodeAt(i) - 97]++;                   // 加入新字符
    sCount[s.charCodeAt(i - pLen) - 97]--;            // 移除旧字符

    if (arraysEqual(sCount, pCount)) res.push(i - pLen + 1);
  }

  return res;
}

// 判断两个频率数组是否相同
function arraysEqual(a, b) {
  for (let i = 0; i < 26; i++) {
    if (a[i] !== b[i]) return false;
  }
  return true;
}

• 时间复杂度：O(n)，其中 n 是字符串 s 的长度；
• 空间复杂度：O(1)，因为数组大小固定为 26（小写英文字母）。