小宋爱睡觉
  • 树
Crucials
2022-03-02

二叉搜索树

# lc230. 二叉搜索树中第k小的元素中等

题目描述

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

示例 1：

img

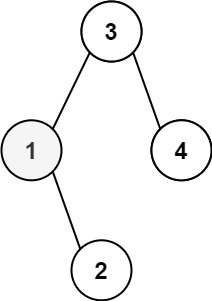
输入：root = [3,1,4,null,2], k = 1

输出：1
1
2
3

示例 2：

img

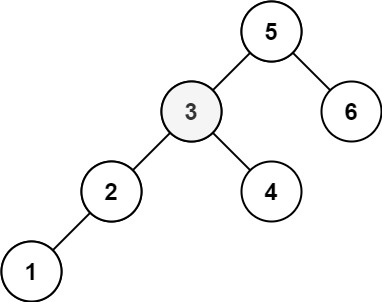
输入：root = [5,3,6,2,4,null,null,1], k = 3

输出：3
1
2
3

迭代中序遍历

var kthSmallest = function(root, k) {
  const stack = []
  while(stack.length || root) {
    while(root) {
      stack.push(root)
      root = root.left
    }
    root = stack.pop()
    if(--k === 0) return root.val

    root = root.right
  }
  return null
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
  • 时间复杂度：O(H+k)，其中 H 指的是树的高度，由于开始遍历之前，要先向下达到叶，当树是一个平衡树时：复杂度为 O(logN+k)。当树是一个不平衡树时：复杂度为 O(N+k)，此时所有的节点都在左子树。
  • 空间复杂度：O(H+k)。当树是一个平衡树时：O(logN+k)。当树是一个非平衡树时：O(N+k)。

递归中序遍历

var kthSmallest = function(root, k) {
    const result = []
    function travel(node){
        if(result.length >= k) return 
        if(node.left){
            travel(node.left)
        }
        result.push(node.val)
        if(node.right){
            travel(node.right)
        }
    }
    travel(root)
    return result[k - 1]
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
  • 时间复杂度：O(n)，其中n是二叉树的节点数，需要遍历了整个树。
  • 空间复杂度：O(n)，用了一个数组存储中序序列。

# 剑指54. 二叉搜索树中第k大的元素中等

题目描述

给定一棵二叉搜索树，请找出其中第k大的节点。

示例 1:

输入: root = [3,1,4,null,2], k = 1

   3
  / \
 1   4
  \
  2

输出: 4
1
2
3
4
5
6
7
8
9

示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 4
1
2
3
4
5
6
7
8
9

采用反向递归中序遍历即可

var kthLargest = function(root, k) {
  const res = []
  const dfs = node => {
    if(!node) return

    dfs(node.right)
    res.push(node.val)
    dfs(node.left)
  }
  dfs(root)

  return res[k - 1]
};
1
2
3
4
5
6
7
8
9
10
11
12
13

时间复杂度:O(n)

空间复杂度:O(n)

迭代

var kthLargest = function(root, k) {
  if(!root) return null
  const stack = []
  while(stack.length || root) {
    while(root) {
      stack.push(root)
      root = root.right
    }
    root = stack.pop()
    if(--k === 0) return root.val
    root = root.left
  }
  return null
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

时间复杂度:O(h + k)

空间复杂度:O(h)

# lc530:二叉搜索树的最小绝对值简单

题目描述

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

示例 1：

img

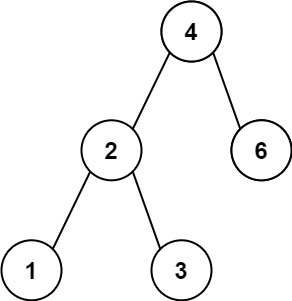
输入：root = [4,2,6,1,3]

输出：1
1
2
3

示例 2：

img

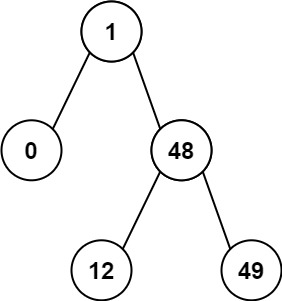
输入：root = [1,0,48,null,null,12,49]

输出：1
1
2
3

递归

var getMinimumDifference = function(root) {
  let pre = null
  let min = +Infinity

  const inorder = node => {
    if(node) {
      inorder(node.left)
      if(pre) {
        let diff = Math.abs(node.val - pre.val)
        min = diff < min ? diff : min
      }
      pre = node
      inorder(node.right)
    }
  }
  inorder(root)
  return min
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

时间复杂度：O(n)，其中 n 为二叉搜索树节点数。每个节点在中序遍历中都会被访问一次且只会被访问一次，因此总时间复杂度为 O(n)。

空间复杂度：O(n)。递归函数的空间复杂度取决于递归的栈深度，而栈深度在二叉搜索树为一条链的情况下会达到 O(n) 级别

迭代

var getMinimumDifference = function(root) {
  if(!root) return 0
  const stack = []
  let pre = null
  let min = +Infinity
  while(stack.length || root) {
    while(root) {
      stack.push(root)
      root = root.left
    }
    root = stack.pop()
    if(pre) {
      min = Math.min(Math.abs(pre.val - root.val), min)
    }
    pre = root
    root = root.right
  }
  return min
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

时间复杂度:O(n)

空间复杂度:O(n)

# lc501. 二叉搜索树中的众数简单

题目描述

给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。

假定 BST 有如下定义：

结点左子树中所含结点的值小于等于当前结点的值

结点右子树中所含结点的值大于等于当前结点的值

左子树和右子树都是二叉搜索树

例如：

给定 BST [1,null,2,2],
   1
    \
     2
    /
   2
返回[2]
1
2
3
4
5
6
7

前序遍历版本

var findMode = function(root) {
  const map = new Map(), res = []
  let max = 0
  const dfs = node => {
    if(!node) return []
    let val = map.get(node.val)
    val ? map.set(node.val, ++val): map.set(node.val, 1)
    max = Math.max(max, map.get(node.val))
    dfs(node.left)
    dfs(node.right)
  }

  dfs(root)
  map.forEach((item, index) => {
    if(max === item) res.push(index)
  })
  return res
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
  • 时间复杂度：O(n)，其中n是这棵树的节点数量，我们需要遍历整棵树。
  • 空间复杂度：O(n)，其中n是这棵树的节点数量，这里需要的是递归的栈空间的空间代价。

中序遍历版本

var findMode = function(root) {  
  let max = 0, count = 0
  let res = []
  let last = null

  const inorder = node => {
    if(node.left) inorder(node.left)

    if (last === node.val) count++
    else count = 1
    last = node.val
    if (count > max) {
      max = count
      res = [node.val]
    } else if (count === max) res.push(node.val)
  
    if(node.right) inorder(node.right)
  }

  inorder(root)
  return res
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

时间复杂度:O(n)

空间复杂度:O(1)

# lc700. 二叉搜索树的搜索简单

题目描述

给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL。

例如

给定二叉搜索树:
        4
       / \
      2   7
     / \
    1   3

和值: 2
你应该返回如下子树:
      2     
     / \   
    1   3
在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回 NULL。
1
2
3
4
5
6
7
8
9
10
11
12
13
// 迭代
var searchBST = function(root, val) {
  while(root) {
    if(root.val === val) return root
    else if (root.val < val) root = root.right
    else root = root.left
  }
  return null
};
// 时间复杂度：O(H)，其中 H 是树高。平均时间复杂度为 O(logN)，最坏时间复杂度为O(N)。
// 空间复杂度：O(1)，恒定的额外空间

// 递归
var searchBST = function(root, val) {
   if(!root){
       return null
   }
   if(root.val === val){
       return root
   }else if(root.val < val){
       return searchBST(root.right, val)
   }else{
       return searchBST(root.left, val)
   }
};
// 时间复杂度：O(H)，其中 H 是树高。平均时间复杂度为 O(logN)，最坏时间复杂度为 O(N)。
// 空间复杂度：O(H)，递归栈的深度为 H。平均情况下深度为 O(logN)，最坏情况下深度为 O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# lc701. 二叉搜索树的插入中等

题目描述

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

img

输入：root = [4,2,7,1,3], val = 5

输出：[4,2,7,1,3,5]
1
2
3

解释：另一个满足题目要求可以通过的树是：

img

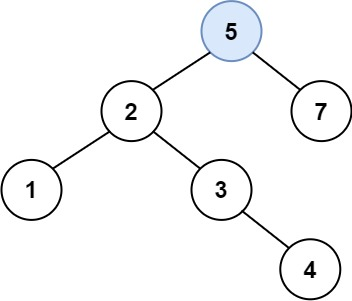
示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25

输出：[40,20,60,10,30,50,70,null,null,25]
1
2
3

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5

输出：[4,2,7,1,3,5]
1
2
3
// 递归
var insertIntoBST = function(root, val) {
  if(!root) return new TreeNode(val)

  if(val < root.val) root.left = insertIntoBST(root.left, val)
  else root.right = insertIntoBST(root.right, val)

  return root
};
// 时间复杂度：O(N)，其中 N 为树中节点数。最坏情况下，需要将值插入到树的最深的叶子结点上，而叶子节点最深为 O(N)。
// 空间复杂度：O(1)。我们只使用了常数大小的空间

// 迭代
var insertIntoBST = function(root, val) {
    if(!root){
        return new TreeNode(val)
    }
    let cur = root
    while(cur){
        if(val > cur.val){
           if(!cur.right){
                cur.right = new TreeNode(val)
                return root
           }else{
               cur = cur.right
           }
        }else{
            if(!cur.left){
                cur.left = new TreeNode(val)
                return root
            }else{
                cur = cur.left
            }
        }
    }
    return root
};
// 时间复杂度：O(N)，其中 N 为树中节点数。最坏情况下，需要将值插入到树的最深的叶子结点上，而叶子节点最深为 O(N)。
// 空间复杂度：O(1)。我们只使用了常数大小的空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

#

上次更新: 2022/03/20, 19:40:28
二叉树的递归

←

Copyright © 2021-2022 粤ICP备2021165371号