链表

快慢指针

# 快慢指针

# lc141. 环形链表简单hot

题目描述

给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。否则，返回 false 。

进阶：

你能用 O(1)（即，常量）内存解决此问题吗？

示例 1：

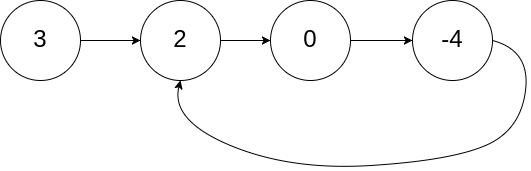
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

1
2
3

示例 2：

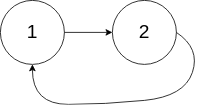
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

1
2
3

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

1
2
3

快慢指针

/**
 * @param {ListNode} head
 * @return {boolean}
 */
var hasCycle = function(head) {
    if(!head || !head.next) return false
    let slow = head.next
    let fast = head.next.next
    while(slow !== fast) {
        // 快指针走得快，如果他提前到null了就没有环
        if(!fast || !fast.next) return false
        fast = fast.next.next
        slow = slow.next
    }
    return true
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

时间复杂度:O(n)

空间复杂度:O(1)

# 142. 环形链表 II中等hot

题目描述

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

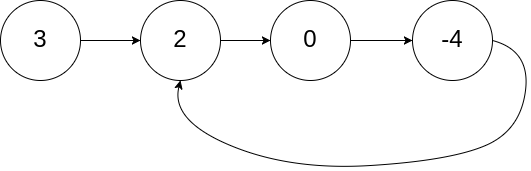
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

1
2
3

示例 2：

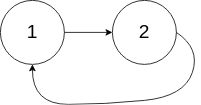
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

1
2
3

示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

1
2
3

思路

从题中我们可以得知 fast 指针比 slow 指针每次多走 1步，这样，在 slow 和 fast 相遇的情况下，假设 slow 走了 k 步，那么 fast 就走了 2k 步

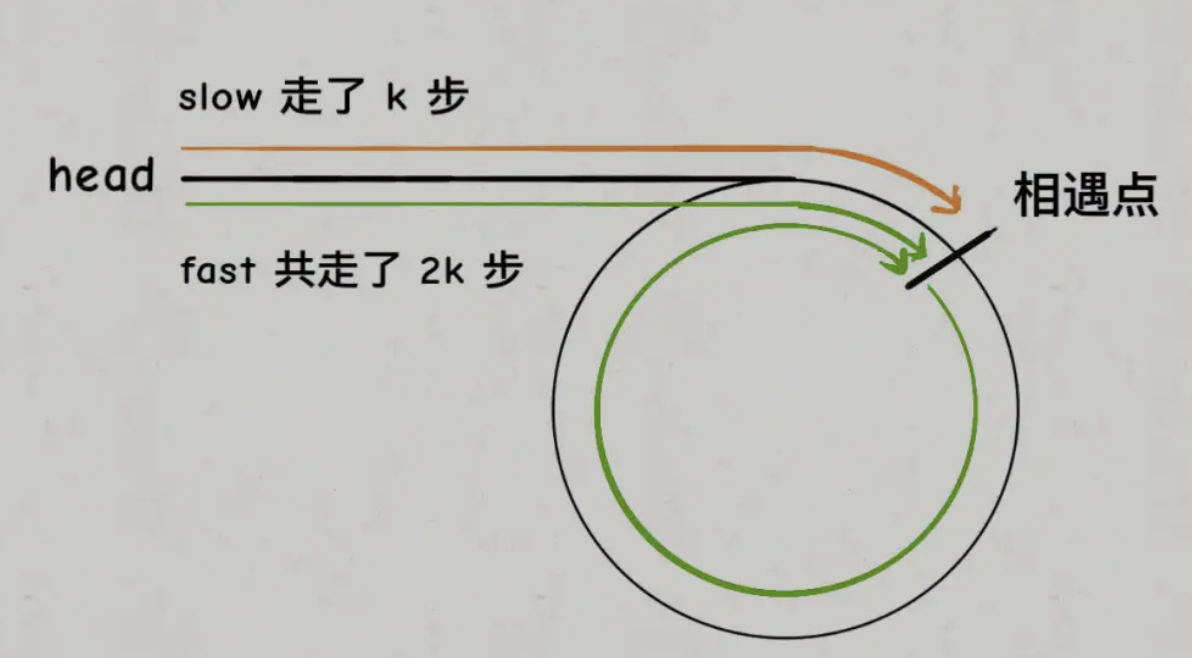
然后按照上图描述的所示，如果我们假设相遇点和环的起点距离是 m 步的话，那么 head到环起点就是 k-m 步，又因为 fast 目前总共走了 2k 步，那么剩下的相遇点到环起点的距离是 k-m 步，和 head 到环起点的步数相同此时，我们将fast 的脚步步伐和 slow 保持一致，直至他们相遇就是环的起点

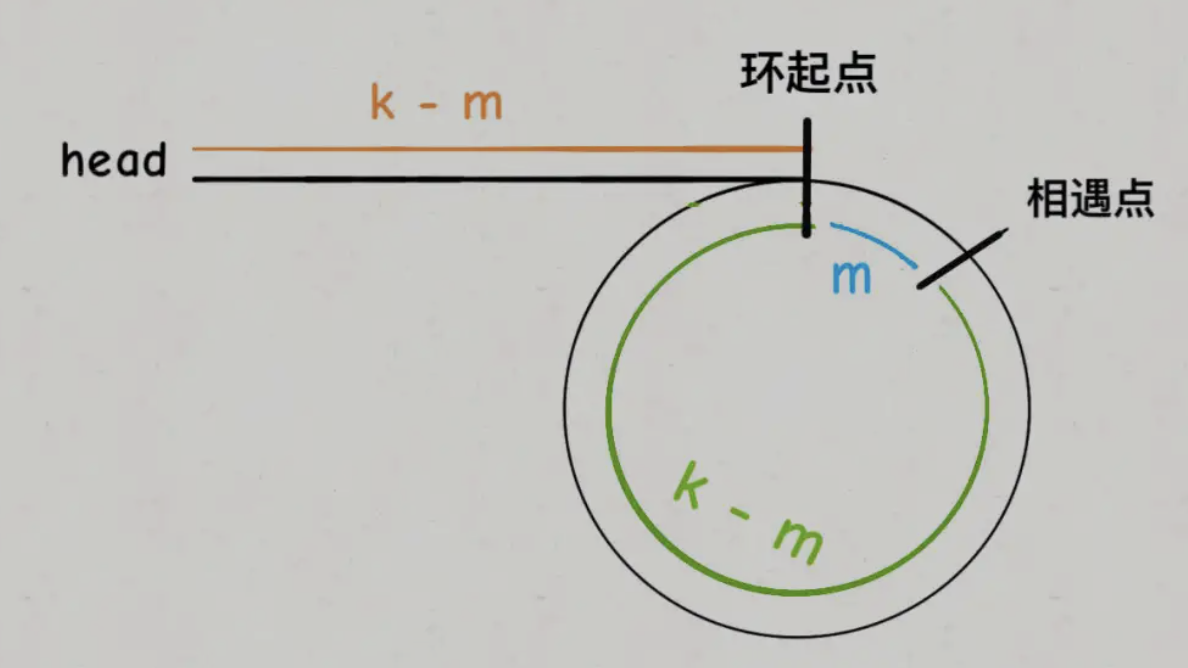
x：从 head 到入环点的距离（非环部分长度）

y：从入环点到 相遇点 的距离（环上的一段）

r：整个环的长度

n：快指针比慢指针多走了 n 圈（每圈是 r）

慢指针走了 slow = x + y

快指针走了 fast = x + y + n * r

快指针走的路是慢指针的两倍 x + y + n * r = 2(x + y)

=> x = nr - y

从 相遇点走 r - y 就会回到入环点（因为整个环长度是 r）

那么 nr - y 就是从相遇点绕 n 圈 + 回到入环点要走的距离

同时，从 head 出发的那个指针也刚好走了 x 步

var detectCycle = function(head) {
  let slow = head;
  let fast = head;

  // 第一步：判断是否有环
  while (fast && fast.next) {
    slow = slow.next;
    fast = fast.next.next;
    if (slow === fast) {
      // 第二步：找环的入口
      let p1 = head;
      let p2 = slow;
      while (p1 !== p2) {
        p1 = p1.next;
        p2 = p2.next;
      }
      return p1; // 或 p2，指向入环点
    }
  }

  return null; // 无环
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

时间复杂度:O(n)

空间复杂度:O(1)

# lc876. 求链表的中间节点简单

题目描述

给定一个头结点为 head 的非空单链表，返回链表的中间结点。

如果有两个中间结点，则返回第二个中间结点。

示例 1：

输入：[1,2,3,4,5]
输出：此列表中的结点 3 (序列化形式：[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
注意，我们返回了一个 ListNode 类型的对象 ans，这样：
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.

1
2
3
4
5

示例 2：

输入：[1,2,3,4,5,6]
输出：此列表中的结点 4 (序列化形式：[4,5,6])
由于该列表有两个中间结点，值分别为 3 和 4，我们返回第二个结点。

1
2
3

思路：

废话少说，这题又是典型的快慢指针，当快指针走到底的时候，慢指针刚好走到一半

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var middleNode = function(head) {
    if(!head && !head.next) return head
    let slow = head
    let fast = head
    while(fast && fast.next) {
        fast = fast.next.next
        slow = slow.next
    }
    return slow
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# lc19. 删除链表的倒数第N个节点中等

题目描述

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

进阶：你能尝试使用一趟扫描实现吗？

示例 1：

输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

1
2

示例 2：

输入：head = [1], n = 1
输出：[]

1
2

示例 3：

输入：head = [1,2], n = 1
输出：[1]

1
2

class ListNode {
  constructor(val, next = null) {
    this.val = val;
    this.next = next;
  }
}

function removeNthFromEnd(head, n) {
  const dummy = new ListNode(0, head);  // 虚拟头结点
  let fast = dummy;
  let slow = dummy;

  // Step 1: fast 先走 n + 1 步
  for (let i = 0; i < n + 1; i++) {
    fast = fast.next;
  }

  // Step 2: fast, slow 一起走
  while (fast) {
    fast = fast.next;
    slow = slow.next;
  }

  // Step 3: 删除 slow.next
  slow.next = slow.next.next;

  return dummy.next;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# lc234. 回文链表简单hot

题目描述

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true；否则，返回 false

示例 1：

输入：head = [1,2,2,1]

输出：true

1
2
3

示例 2：

输入：head = [1,2]

输出：false

1
2
3

法二快慢指针

快指针走两步慢指针走一步，慢指针边走边反转链表然后当快指针走到尾的时候，开始比较值是否一样

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {boolean}
 */
var isPalindrome = function(head) {
  let pre = null
  let slow = fast = head
  let next = null
  while(fast && fast.next) {
    // 快指针走两步
    fast = fast.next.next
    // 慢指针边走边反转链表
    next = slow.next
    slow.next = pre

    pre = slow
    slow = next
  }
  // 如果链表为奇数 慢指针再走一步
  if(fast) slow = slow.next
  // 开始比较是否为回文
  while(slow) {
    if(slow.val !== pre.val) return false
    slow = slow.next
    pre = pre.next
  }
  return true
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

时间复杂度O(n)

空间复杂度O(n)

# lc1721.交换链表中的节点中等

给你链表的头节点 head 和一个整数 k

交换链表正数第 k个节点和倒数第 k 个节点的值后，返回链表的头节点（链表从 1 开始索引）。

示例 1：

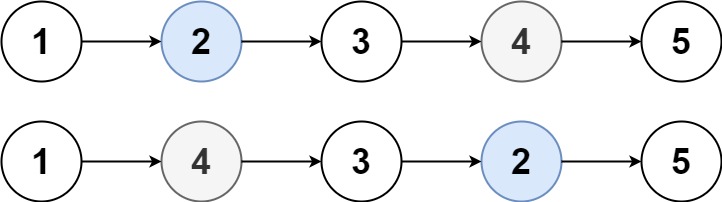
输入：head = [1,2,3,4,5], k = 2

输出：[1,4,3,2,5]

1
2
3

示例 2：

输入：head = [7,9,6,6,7,8,3,0,9,5], k = 5

输出：[7,9,6,6,8,7,3,0,9,5]

1
2
3

示例 3：

输入：head = [1], k = 1

输出：[1]

1
2
3

示例 4：

输入：head = [1,2], k = 1

输出：[2,1]

1
2
3

示例 5：

输入：head = [1,2,3], k = 2

输出：[1,2,3]

1
2
3

思路快慢指针

就是采用快慢指针，先让快指针走k步，然后记录快指针的位置，然后快慢指针一起走，走到底的时候慢指针就是倒数第k个数，然后交换

/**
 * @param {ListNode} head
 * @param {number} k
 * @return {ListNode}
 */
var swapNodes = function(head, k) {
  if(!head || !head.next) return head
  let dummyHead = new ListNode(null)
  dummyHead.next = head

  let fast = slow = dummyHead
  let cur = null

  while(k--) {
    fast = fast.next    
  }
  // 记录第k位的值
  cur = fast
  while(fast) {
    slow = slow.next
    fast = fast.next
  }
  [cur.val, slow.val] = [slow.val, cur.val]

  return dummyHead.next
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

时间复杂度O(n)

空间复杂度O(1)

# lc143. 重排链表中等hot

题目描述

给定一个单链表 L 的头节点 head ，单链表 L 表示为：

L0 → L1 → … → Ln-1 → Ln

请将其重新排列后变为：

L0 → Ln → L1 → Ln-1 → L2 → Ln-2 → …

不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

示例 1:

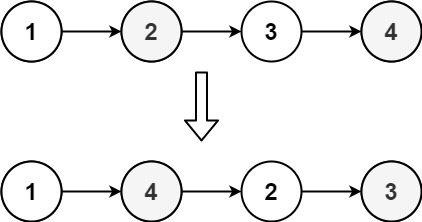
输入: head = [1,2,3,4]

输出: [1,4,2,3]

1
2
3

示例 2:

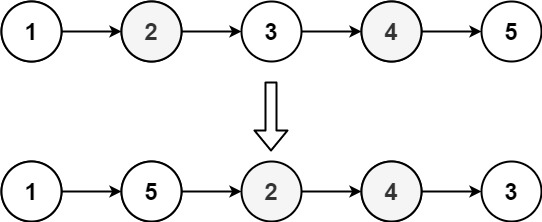
输入: head = [1,2,3,4,5]

输出: [1,5,2,4,3]

1
2
3

思路

先利用快慢指针找到中点，再断开成两个链表，后一个链表进行反转，然后依次插入

var reorderList = function(head) {
  if(!head || !head.next) return 
  let fast = slow = head

  while(fast && fast.next) {
    fast = fast.next.next 
    slow = slow.next
  }
  //断开前后两个链表
  fast = slow.next
  slow.next = null
  slow = head 

  // 反转链表
  let pre = null
  let cur = fast
  while(cur) {
    let next = cur.next

    cur.next = pre
    pre = cur
    cur = next
  }
  // 快指针指向反转后的链表
  fast = pre

  while(fast) {
    let slowNext = slow.next
    let fastNext = fast.next

    slow.next = fast
    fast.next = slowNext
    slow = slowNext
    fast = fastNext
  }
  return head
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

时间复杂度O(n)

空间复杂度O(1)

上次更新: 2025/06/08, 23:39:58

← 递归双指针→