其他

lc31. 下一个排列中等hot

题目描述

整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。

• 例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。

整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

• 例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
• 类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
• 而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。

给你一个整数数组 nums ，找出 nums 的下一个排列。

必须** 原地 (opens new window)**修改，只允许使用额外常数空间。

示例 1：

输入：nums = [1,2,3]
输出：[1,3,2]

示例 2：

输入：nums = [3,2,1]
输出：[1,2,3]

示例 3：

输入：nums = [1,1,5]
输出：[1,5,1]

思路

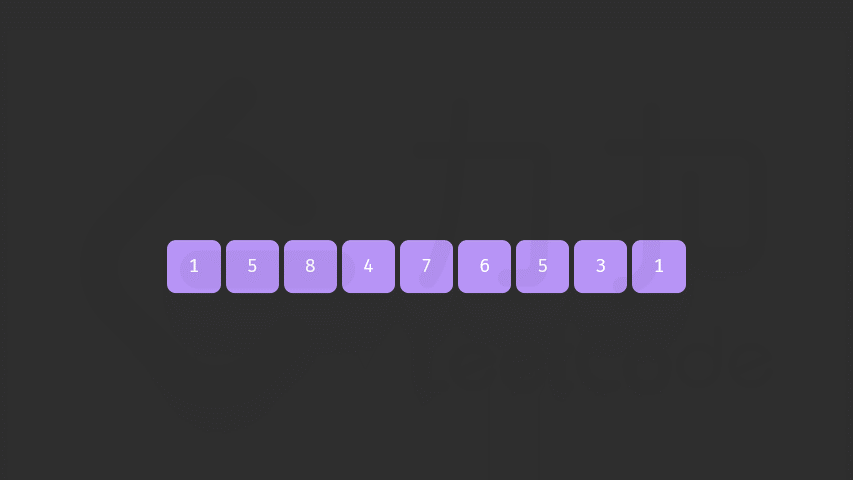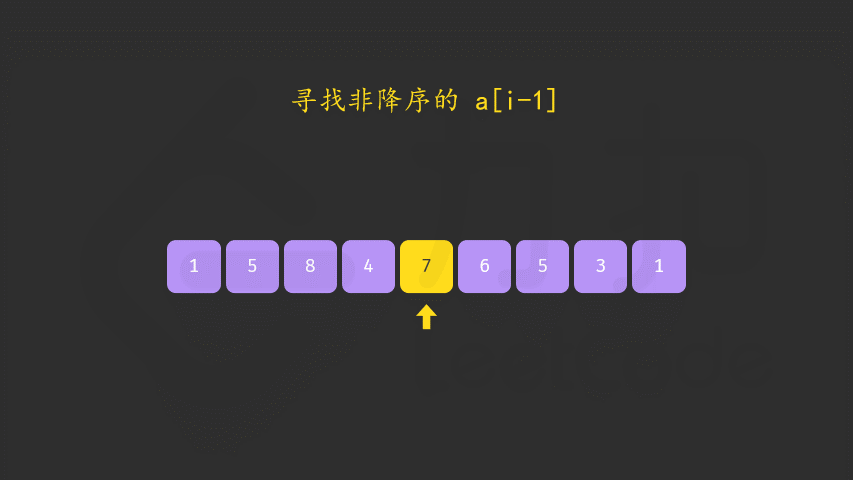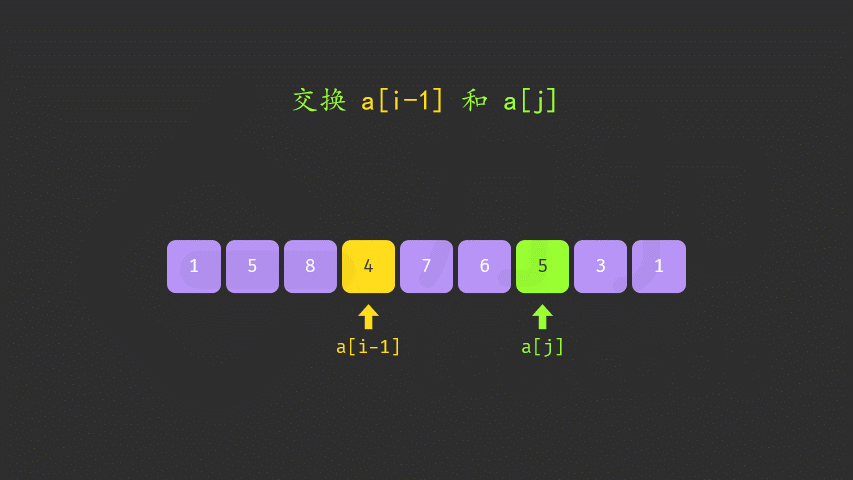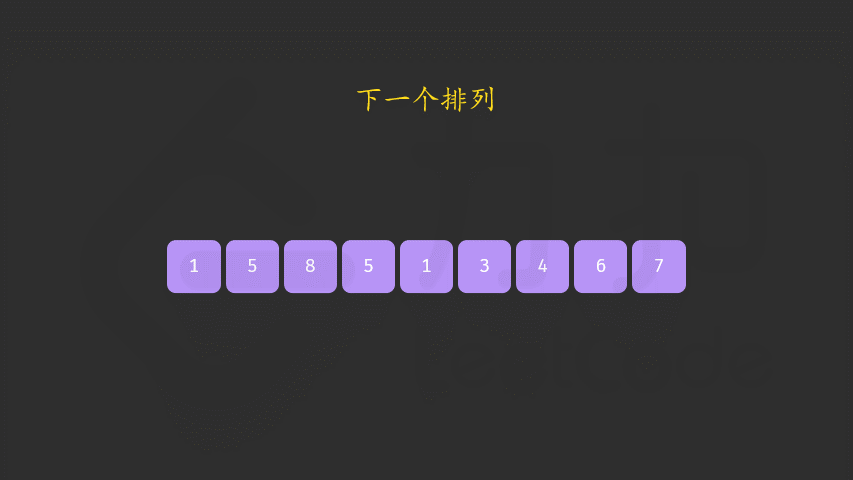
• 先倒序找到在i后面比nums[i]大的数
• 再找到比cur大一点点的数 两者交换
• 因为i后面是倒叙的 若让他尽可能的小，转成升序

function nextPermutation(nums) {
  const n = nums.length;
  let i = n - 2;

  // 第一步：从右往左找到第一个 nums[i] < nums[i + 1]
  while (i >= 0 && nums[i] >= nums[i + 1]) {
    i--;
  }

  if (i >= 0) {
    // 第二步：从右往左找第一个大于 nums[i] 的数
    let j = n - 1;
    while (j >= 0 && nums[j] <= nums[i]) {
      j--;
    }

    // 交换 nums[i] 和 nums[j]
    [nums[i], nums[j]] = [nums[j], nums[i]];
  }

  // 第三步：反转 i+1 到末尾
  reverse(nums, i + 1, n - 1);
}

// 辅助函数：原地反转数组的一段
function reverse(arr, left, right) {
  while (left < right) {
    [arr[left], arr[right]] = [arr[right], arr[left]];
    left++;
    right--;
  }
}

时间复杂度:O(n),

1. 寻找第一个下降点（从右往左找 nums[i] < nums[i+1]） → 最多走一遍数组，O(n)
2. 寻找第一个大于 nums[i] 的数（从右往左找 nums[j] > nums[i]） → 也是一次遍历，O(n)，但不会比第一次更多
3. 反转后缀部分 → 最多反转整个数组尾部，O(n)

👉 所以总时间复杂度是 O(n + n + n)，简化后为：

✅ 时间复杂度：O(n)

空间复杂度:O(1)

lc130. 被围绕的区域中等

题目描述

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：

输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：

输入：board = [["X"]]
输出：[["X"]]

思路：DFS

类似的先对四个边做判断并标记为A，再次进行遍历，如果是A说明是边界情况，那么还原为O

var solve = function (board) {
  let rows = board.length;
  if (rows == 0) return;
  let cols = board[0].length;
  const dfs = (i, j, board) => {
      if (i < 0 || j < 0 || i >= rows || j >= cols || board[i][j] !== 'O') {
          return;
      } 
      // 判断边界的o是否与内部的o是连接的，连接则不能构成岛屿
      board[i][j] = 'A';
      dfs(i + 1, j, board);
      dfs(i - 1, j, board)
      dfs(i, j + 1, board)
      dfs(i, j - 1, board)
  }

  for (let i = 0; i < rows; i++) {
      dfs(i, 0, board);
      dfs(i, cols - 1, board);
  }
  for (let i = 1; i < cols - 1; i++) {
      dfs(0, i, board);
      dfs(rows - 1, i, board);
  }
  for (let i = 0; i < rows; i++) {
      for (let j = 0; j < cols; j++) {
          if (board[i][j] == 'A') {
              board[i][j] = 'O'
          } else if (board[i][j] == 'O') {
              board[i][j] = 'X'
          }
      }
  }

};

时间复杂度:O(n * m)

空间复杂度:O(n * m)

lc200. 岛屿数量中等hot

题目描述

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

思路

遍历每个格子

一旦遇到 '1'，就从这个位置出发，用 DFS 把和它相连的所有 '1' 都“淹没掉”（设成 '0'）

每次成功触发一轮 DFS，就说明发现了一个新的岛屿

var numIslands = function(grid) {
  if (!grid || grid.length === 0) return 0;

  const rows = grid.length;
  const cols = grid[0].length;
  let count = 0;

  function dfs(r, c) {
    // 越界 或 遇到水（0） 就返回
    if (
      r < 0 || r >= rows ||
      c < 0 || c >= cols ||
      grid[r][c] === '0'
    ) {
      return;
    }

    // 将当前陆地标记为已访问
    grid[r][c] = '0';

    // 继续访问四个方向
    dfs(r + 1, c); // 下
    dfs(r - 1, c); // 上
    dfs(r, c + 1); // 右
    dfs(r, c - 1); // 左
  }

  for (let r = 0; r < rows; r++) {
    for (let c = 0; c < cols; c++) {
      if (grid[r][c] === '1') {
        count++;     // 找到一个新岛屿
        dfs(r, c);   // 开始淹没整个岛屿
      }
    }
  }

  return count;
};

时间复杂度:O(mn)

空间复杂度:递归栈的深度，最坏的是全是陆地，O(mn),最好是递归深度很小O(1),平均是O(min(m,n))

BFS

遍历每个格子

每当遇到 '1'，岛屿计数 +1，进入 BFS：

• 把这个位置加入队列
• 不断从队列取出一个位置，访问它的上下左右
• 如果邻居是 '1'，也入队并设为 '0'，避免重复访问

function numIslands(grid) {
  if (!grid || grid.length === 0) return 0;

  const rows = grid.length;
  const cols = grid[0].length;
  let count = 0;

  const directions = [
    [1, 0],  // 下
    [-1, 0], // 上
    [0, 1],  // 右
    [0, -1], // 左
  ];

  function bfs(r, c) {
    const queue = [];
    queue.push([r, c]);
    grid[r][c] = '0'; // 标记为已访问

    while (queue.length > 0) {
      const [curR, curC] = queue.shift();

      for (const [dr, dc] of directions) {
        const newR = curR + dr;
        const newC = curC + dc;

        if (
          newR >= 0 && newR < rows &&
          newC >= 0 && newC < cols &&
          grid[newR][newC] === '1'
        ) {
          queue.push([newR, newC]);
          grid[newR][newC] = '0'; // 马上标记，防止重复入队
        }
      }
    }
  }

  for (let r = 0; r < rows; r++) {
    for (let c = 0; c < cols; c++) {
      if (grid[r][c] === '1') {
        count++;
        bfs(r, c); // 淹没这一整块岛屿
      }
    }
  }

  return count;
}

695. 岛屿的最大面积中等hot

题目描述

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

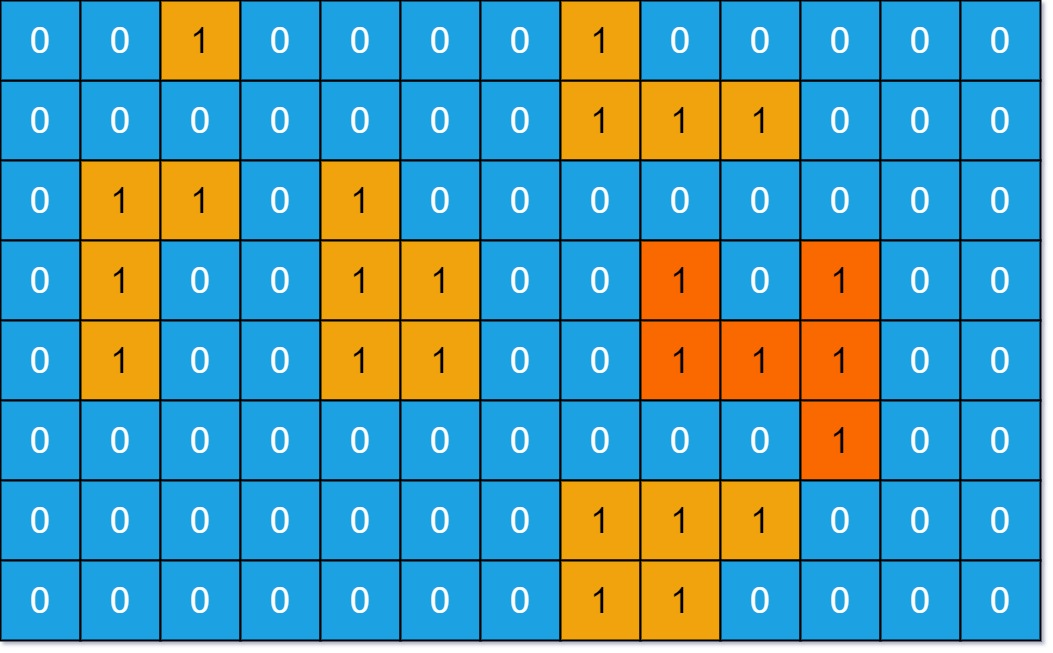
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

dfs

找到1，然后向上下左右发散

/**
 * @param {number[][]} grid
 * @return {number}
 */
var maxAreaOfIsland = function(grid) {
  const m = grid.length;
  const n = grid[0].length;
  let maxArea = 0;

  // DFS 函数，返回以 (i, j) 开始的岛屿面积
  function dfs(i, j) {
    // 越界 或 遇到水（0）就返回 0
    if (i < 0 || j < 0 || i >= m || j >= n || grid[i][j] === 0) {
      return 0;
    }

    // 标记访问过的点为 0
    grid[i][j] = 0;

    // 四个方向探索
    return 1 +
      dfs(i + 1, j) +
      dfs(i - 1, j) +
      dfs(i, j + 1) +
      dfs(i, j - 1);
  }

  // 遍历整个网格
  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (grid[i][j] === 1) {
        maxArea = Math.max(maxArea, dfs(i, j));
      }
    }
  }

  return maxArea;
};

时间复杂度:O(mn)

空间复杂度:O(mn)

bfs

/**
 * @param {number[][]} grid
 * @return {number}
 */
var maxAreaOfIsland = function(grid) {
  const m = grid.length;
  const n = grid[0].length;
  let maxArea = 0;

  const directions = [
    [0, 1], [1, 0], [0, -1], [-1, 0]
  ];

  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (grid[i][j] === 1) {
        let area = 0;
        const queue = [[i, j]];
        grid[i][j] = 0; // 标记为已访问

        while (queue.length > 0) {
          const [x, y] = queue.shift();
          area++;

          for (const [dx, dy] of directions) {
            const nx = x + dx;
            const ny = y + dy;

            if (
              nx >= 0 && nx < m &&
              ny >= 0 && ny < n &&
              grid[nx][ny] === 1
            ) {
              queue.push([nx, ny]);
              grid[nx][ny] = 0; // 标记为已访问
            }
          }
        }

        maxArea = Math.max(maxArea, area);
      }
    }
  }

  return maxArea;
};

时间复杂度:O(mn)

空间复杂度:O(mn)

lc26. 删除有序数组的重复项简单

题目描述

给你一个有序数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参做任何拷贝
int len = removeDuplicates(nums);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

思路：

设置一个变量len，作用是标注每次处理nums数组后共有几个不重复的数字

因为是有序数组，所以nums数组遇到相同的跳过，找到后一个不相同的，然后把不相同的赋值给len 然后len++

var removeDuplicates = function(nums) {
  let len = 1
  for(let i = 1; i < nums.length; i++) {
    if(nums[i] === nums[i - 1]) {
      continue
    }
    nums[len++] = nums[i]
  }
  return len
};

lc384. 打乱数组

题目描述

给你一个整数数组 nums ，设计算法来打乱一个没有重复元素的数组。打乱后，数组的所有排列应该是 等可能 的。

实现 Solution class:

• Solution(int[] nums) 使用整数数组 nums 初始化对象
• int[] reset() 重设数组到它的初始状态并返回
• int[] shuffle() 返回数组随机打乱后的结果

示例 1：

输入
["Solution", "shuffle", "reset", "shuffle"]
[[[1, 2, 3]], [], [], []]
输出
[null, [3, 1, 2], [1, 2, 3], [1, 3, 2]]

解释
Solution solution = new Solution([1, 2, 3]);
solution.shuffle();    // 打乱数组 [1,2,3] 并返回结果。任何 [1,2,3]的排列返回的概率应该相同。例如，返回 [3, 1, 2]
solution.reset();      // 重设数组到它的初始状态 [1, 2, 3] 。返回 [1, 2, 3]
solution.shuffle();    // 随机返回数组 [1, 2, 3] 打乱后的结果。例如，返回 [1, 3, 2]

洗牌算法

var Solution = function(nums) {
  this.nums = nums
};

/**
 * @return {number[]}
 */
Solution.prototype.reset = function() {
  return this.nums
};

/**
 * @return {number[]}
 */
Solution.prototype.shuffle = function() {
  const res = [...this.nums]
  for(let i = 0; i < res.length; i++) {
    let index = Math.floor((i + 1)* Math.random());
    [res[index],res[i]] = [res[i],res[index]]
  }
  return res
};

lc134. 加油站中等

题目描述

在一条环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。

说明:

• 如果题目有解，该答案即为唯一答案。
• 输入数组均为非空数组，且长度相同。
• 输入数组中的元素均为非负数。

示例 1:

输入: 
gas  = [1,2,3,4,5]
cost = [3,4,5,1,2]

输出: 3

解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

示例 2:

输入: 
gas  = [2,3,4]
cost = [3,4,3]

输出: -1

解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周。

思路

1. 计算总剩余量
2. 找出总剩余量最低点

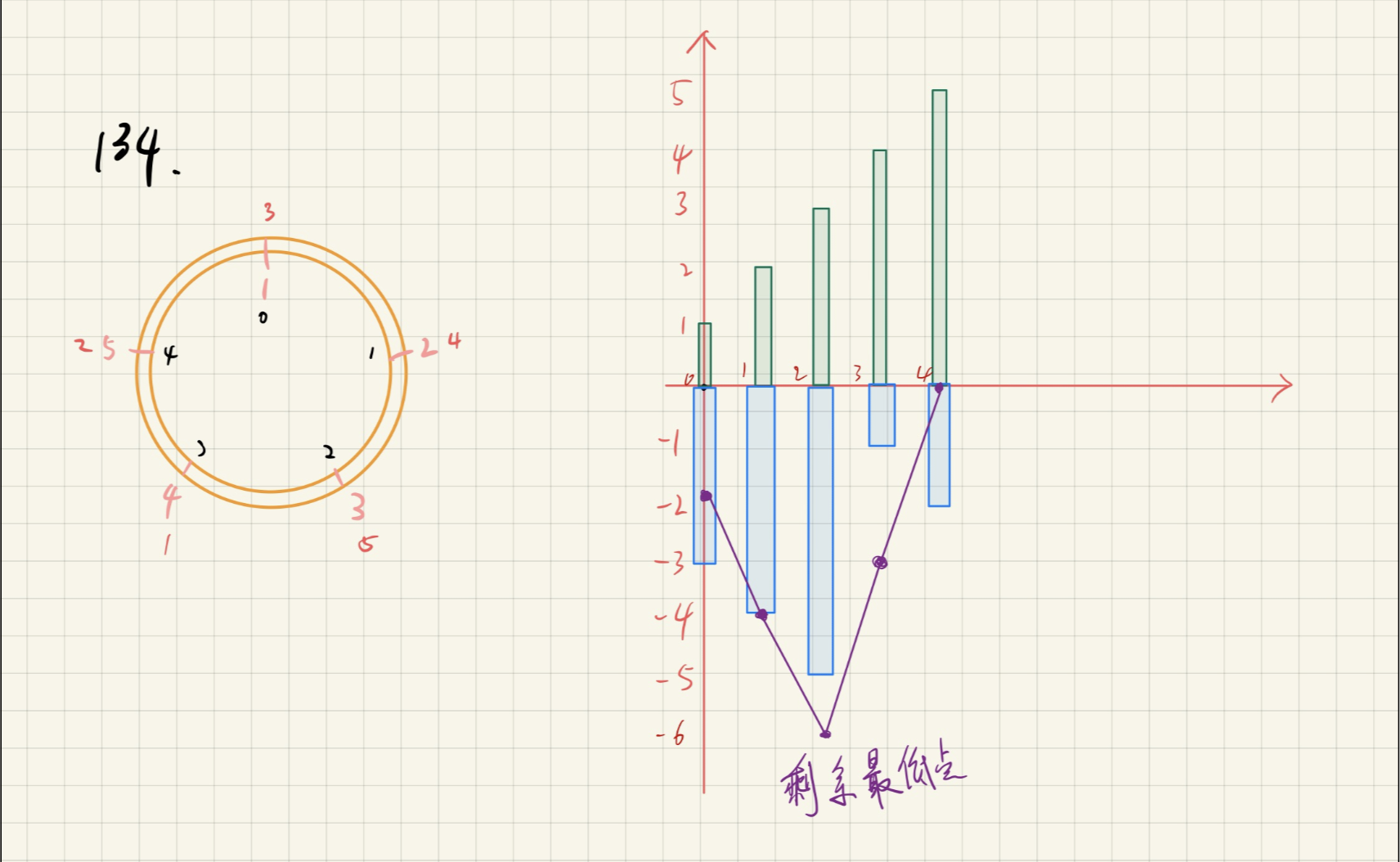
如果最低点的后面一个加油站都不能满足绕一圈的话，那就没有加油站可以满足了

var canCompleteCircuit = function(gas, cost) {
    const n = gas.length
    let innage = 0 // 剩余总量
    let minInnage = Number.MAX_VALUE // 剩余油量最低点
    let ret = 0
    for(let i = 0; i < n; i++){
        innage += gas[i] - cost[i]
        if(innage < minInnage){
            minInnage = innage
            ret = (i + 1) % n // 最低点的下一个点 就是最合适的出发点
        }
    }
    return innage < 0 ? -1 : ret 
};

lc146. LRU 缓存中等top

题目描述

请你设计并实现一个满足 LRU (最近最少使用) 缓存 (opens new window) 约束的数据结构。

实现 LRUCache 类：

• LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
• int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
• void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

class DLinkedNode {
  constructor(key = 0, value = 0) {
    this.key = key;
    this.value = value;
    this.prev = null;
    this.next = null;
  }
}

class LRUCache {
  constructor(capacity) {
    this.capacity = capacity;
    this.cache = new Map(); // key -> node
    // 使用伪头部和伪尾部简化边界操作
    this.head = new DLinkedNode();
    this.tail = new DLinkedNode();
    this.head.next = this.tail;
    this.tail.prev = this.head;
  }

  _addNode(node) {
    // 把节点加到 head 后面（最前面）
    node.prev = this.head;
    node.next = this.head.next;

    this.head.next.prev = node;
    this.head.next = node;
  }

  _removeNode(node) {
    // 删除节点
    const prev = node.prev;
    const next = node.next;

    prev.next = next;
    next.prev = prev;
  }

  _moveToHead(node) {
    // 移动节点到头部
    this._removeNode(node);
    this._addNode(node);
  }

  _popTail() {
    // 弹出尾部节点
    const res = this.tail.prev;
    this._removeNode(res);
    return res;
  }

  get(key) {
    const node = this.cache.get(key);
    if (!node) return -1;

    // 移动到头部表示最近访问
    this._moveToHead(node);
    return node.value;
  }

  put(key, value) {
    let node = this.cache.get(key);

    if (node) {
      // 更新值并移动到头部
      node.value = value;
      this._moveToHead(node);
    } else {
      node = new DLinkedNode(key, value);
      this.cache.set(key, node);
      this._addNode(node);

      if (this.cache.size > this.capacity) {
        // 移除尾部节点（最久未用）
        const tail = this._popTail();
        this.cache.delete(tail.key);
      }
    }
  }
}

lc54. 螺旋矩阵中等hot

题目描述

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

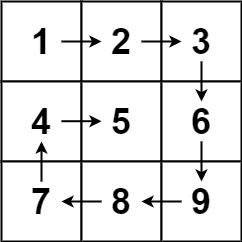
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

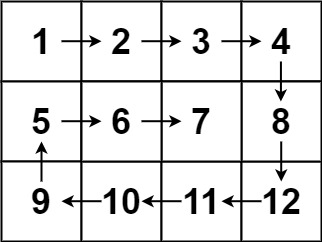
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

思路

var spiralOrder = function (matrix) {
  const arr = [];
  let left = 0,
    top = 0;
  let right = matrix[0].length - 1,
    down = matrix.length - 1;

  while (true) {
    for (let i = left; i <= right; i++) {
      arr.push(matrix[top][i]);
    }
    top++;
    if (top > down) break;
    for (let i = top; i <= down; i++) {
      arr.push(matrix[i][right]);
    }
    right--;
    if (left > right) break;
    for (let i = right; i >= left; i--) {
      arr.push(matrix[down][i]);
    }
    down--;
    if (top > down) break;
    for (let i = down; i >= top; i--) {
      arr.push(matrix[i][left]);
    }
    left++;
    if (left > right) break;
  }
  return arr;
};

lc59. 螺旋矩阵 II中等

题目描述

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

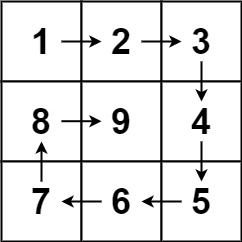
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

思路

跟上题一毛一样

var generateMatrix = function(n) {
  let left = 0, top = 0
  let right = n - 1, down = n - 1
  let cur = 1
  const res = new Array()
  for(let i = 0; i < n; i++) {
    res[i] = new Array()
  }

  while(true) {
    for(let i = left; i <= right; i++) {
      res[top][i] = cur
      cur++
    }
    top++

    if(top > down) break
    for(let i = top; i <= down; i++) {
      res[i][right] = cur
      cur++
    }
    right--

    if(right < left) break
    for(let i = right; i >= left; i--) {
      res[down][i] = cur
      cur++
    }
    down--

    if(down < top) break
    for(let i = down; i >= top; i--) {
      res[i][left] = cur
      cur++
    }
    left++

    if(left > right) break
  }
  return res
};

lc189. 轮转数组中等

题目描述

给你一个数组，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

思路

步骤如下：

1. 整体反转：[7,6,5,4,3,2,1]
2. 反转前 k 个元素（即 [7,6,5] → [5,6,7]）
3. 反转后 n - k 个元素（即 [4,3,2,1] → [1,2,3,4]）

function rotate(nums, k) {
  const n = nums.length;
  k = k % n; // 防止 k 大于数组长度

  reverse(nums, 0, n - 1);
  reverse(nums, 0, k - 1);
  reverse(nums, k, n - 1);
}

function reverse(arr, left, right) {
  while (left < right) {
    [arr[left], arr[right]] = [arr[right], arr[left]];
    left++;
    right--;
  }
}

时间复杂度：O(n)

空间复杂度：O(1)（原地修改）

lc36. 有效的数独中等

题目描述

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

1. 数字 1-9 在每一行只能出现一次。
2. 数字 1-9 在每一列只能出现一次。
3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

• 一个有效的数独（部分已被填充）不一定是可解的。
• 只需要根据以上规则，验证已经填入的数字是否有效即可。
• 空白格用 '.' 表示。

示例 1：

输入：board = 
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：true

示例 2：

输入：board = 
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：false
解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

思路

就是判断3x3里面有没有重复的数字 && 每一行有没有重复数字 && 每一列有没有重复数字

var isValidSudoku = function(board) {
  for(let i = 0; i < 9; i++) {
    if(!verify(board[i])) return false
    if(!verify(getCol(board, i))) return false
    for(let j = 0; j < 9; j++) {
      if(i % 3 === 0 && j % 3 === 0 && !verify(get3x3(board, i, j))) return false
    }
  }
  return true
};

function getCol(nums, index) {
  const res = []
  for(let i = 0; i < nums.length; i++) {
    res.push(nums[i][index])
  }
  return res
}

function get3x3(nums, row, col) {
  const res = []
  for(let i = row; i < row + 3; i++) {
    for(let j = col; j < col + 3; j++) {
      res.push(nums[i][j])
    }
  }
  return res
}

function verify(nums) {
  const validateMap = new Map()
  const isExist = (map, item) => {
    if(map.has(item) && map.get(item) !== '.') return false
    else {
      map.set(item, item) 
      return true
    } 
  }
  return nums.every(num => isExist(validateMap, num))
}

lc48. 旋转图像中等hot

题目描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 (opens new window) 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

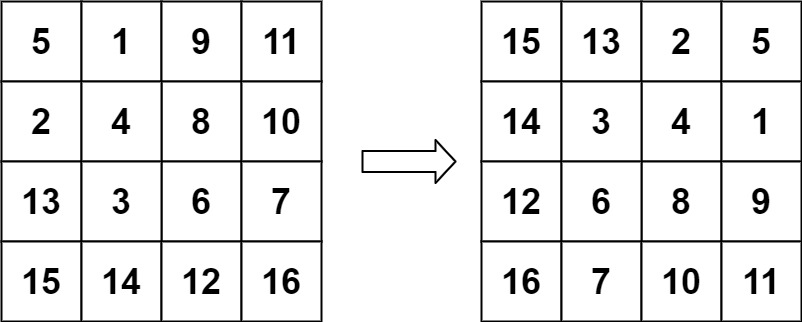
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

思路

首先输入

1 2 3
4 5 6
7 8 9

通过交换matrix[i][j], matrix[j][i] 得到

1 4 7
2 5 8
3 6 9

最后将得到每组数组倒序排列即可

7 4 1
8 5 2
9 6 3

var rotate = function(matrix) {
  for(let i = 0; i < matrix.length; i++) {
    for(let j = i; j < matrix.length; j++) {
      [matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]]
    }
  }
  return matrix.map(item => item.reverse())
};

lc73. 矩阵置零中等

题目描述

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 (opens new window) 算法

示例 1：

输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

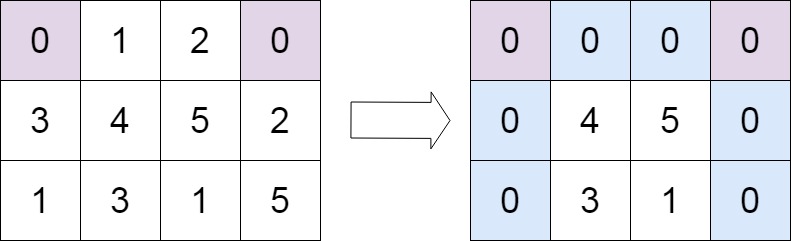
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

思路

暴力法，用时间换空间

function setZeroes(matrix) {
  const m = matrix.length;
  const n = matrix[0].length;

  let firstRowHasZero = false;
  let firstColHasZero = false;

  // Step 1: 标记第一行/列是否需要清零
  for (let i = 0; i < m; i++) {
    if (matrix[i][0] === 0) firstColHasZero = true;
  }
  for (let j = 0; j < n; j++) {
    if (matrix[0][j] === 0) firstRowHasZero = true;
  }

  // Step 2: 用第一行/列作为标记空间
  for (let i = 1; i < m; i++) {
    for (let j = 1; j < n; j++) {
      if (matrix[i][j] === 0) {
        matrix[i][0] = 0;
        matrix[0][j] = 0;
      }
    }
  }

  // Step 3: 根据标记清零
  for (let i = 1; i < m; i++) {
    for (let j = 1; j < n; j++) {
      if (matrix[i][0] === 0 || matrix[0][j] === 0) {
        matrix[i][j] = 0;
      }
    }
  }

  // Step 4: 最后处理第一行和第一列
  if (firstColHasZero) {
    for (let i = 0; i < m; i++) matrix[i][0] = 0;
  }

  if (firstRowHasZero) {
    for (let j = 0; j < n; j++) matrix[0][j] = 0;
  }
}

时间复杂度:O(mn)

空间复杂度:O(1)

lc179. 最大数中等hot

题目描述

给定一组非负整数 nums，重新排列每个数的顺序（每个数不可拆分）使之组成一个最大的整数。

注意： 输出结果可能非常大，所以你需要返回一个字符串而不是整数。

示例 1：

输入：nums = [10,2]
输出："210"

示例 2：

输入：nums = [3,30,34,5,9]
输出："9534330"

示例 3：

输入：nums = [1]
输出："1"

示例 4：

输入：nums = [10]
输出："10"

思路:sort

var largestNumber = function(nums) {
  nums = nums.map(item => String(item))

  nums.sort((a, b) => {
    let res1 = a + b
    let res2 = b + a
    return res2 - res1
  })
  if(nums[0] === '0') return '0'
  return nums.join('')
};

快排

var largestNumber = function (nums) {
  quickSort(nums, 0, nums.length - 1);
  return nums[0] == "0" ? "0" : nums.join("");
};
function quickSort(nums, start, end) {
  if (start >= end) return;
  var index = start;
  var pivot = nums[start];
  for (let i = start + 1; i <= end; i++) {
    if (nums[i] + "" + pivot > pivot + "" + nums[i]) {
      index++;
      swap(nums, index, i);
    }
  }
  swap(nums, index, start);
  quickSort(nums, start, index - 1);
  quickSort(nums, index + 1, end);
}
function swap(nums, l, r) {
  var temp = nums[l];
  nums[l] = nums[r];
  nums[r] = temp;
}

lc169. 多数元素/超过一半的数字简单hot

题目描述

给定一个大小为 n 的数组，找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：

输入：[3,2,3]
输出：3

示例 2：

输入：[2,2,1,1,1,2,2]
输出：2

思路一

用map计数

var majorityElement = function(nums) {
  let map = new Map()
  let count = Math.ceil(nums.length / 2)
  for(let i = 0; i < nums.length; i++) {
    if(!map.has(nums[i])) map.set(nums[i], 1)
    else {
      map.set(nums[i], map.get(nums[i]) + 1)
    }
  }
  for(let [key, val] of map) {
    if(val >= count) return key
  }
};

时间复杂度:O(n)

空间复杂度:O(n)

思路二：摩尔投票法

声明一个变量vote,因为超过半数这种特殊性我们可以遍历数组

• 令vote等于1，final等于第一个值nums[i]
  • 如果nums[i] === nums[i + 1]，vote加一，final不变
  • 如果后面的值不相等，vote减一
• 如果是vote减为0了，他会等于再下一个值 nums[i + 2] vote重新置为1

这是因为超过半数的数字一定会把剩下数字给抵消掉的

var majorityElement = function(nums) {
  if(!nums.length) return null
  let vote = 1
  let final = nums[0]
  for(let i = 1; i < nums.length; i++) {
    if(vote === 0) {
      vote = 1
      final = nums[i]
    } else {
      if(nums[i] === final) vote++  
      else vote--
    }
  }
  return final
};

时间复杂度:O(n)

空间复杂度:O(1)

思路三：排序后的中位数

同样也是因为超过半数的特殊性，使得排序后的众数一定占据了中位数

var majorityElement = function(nums) {
    nums.sort((a,b)=>a-b);
    return nums[Math.floor(nums.length/2)];
};

时间复杂度:O(nlogn)

空间复杂度:O(1ogn)

lc238. 除自身以外数组的乘积中等

题目描述

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请**不要使用除法，**且在 O(*n*) 时间复杂度内完成此题。

示例 1:

输入: nums = [1,2,3,4]
输出: [24,12,8,6]

示例 2:

输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]

题解：

prefix[i] = a0 * a1 * ... * a(i-1)

suffix[i] = a(i+1) * a(i+2) * ... * an

等于前缀积 * 后缀积

function productExceptSelf(nums) {
  const n = nums.length;
  const answer = new Array(n).fill(1);

  // 1. 计算左侧乘积
  let left = 1;
  for (let i = 0; i < n; i++) {
    answer[i] = left;
    left *= nums[i];
  }

  // 2. 计算右侧乘积，并乘到结果中
  let right = 1;
  for (let i = n - 1; i >= 0; i--) {
    answer[i] *= right;
    right *= nums[i];
  }

  return answer;
}

时间复杂度:O(n);

额外空间复杂度:O(1);

lc289. 生命游戏中等

题目描述

根据 百度百科 (opens new window) ， 生命游戏 ，简称为 生命 ，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

1. 如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
2. 如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
3. 如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
4. 如果死细胞周围正好有三个活细胞，则该位置死细胞复活；

下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。

示例 1：

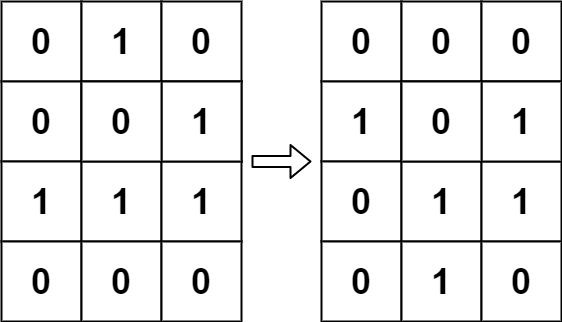
输入：board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
输出：[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

示例 2：

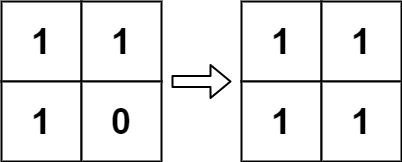
输入：board = [[1,1],[1,0]]
输出：[[1,1],[1,1]]

思路一：额外空间

这个题目有一个坑，某一轮更改的数字的周围的个数的计数是按照最初的数组计算，而不是按照上一轮的计算

创建一个额外的数组，然后对每个元素遍历，看看周围八个元素的情况

var gameOfLife = function(board) {
  if(!board.length) return
  let rows = board.length
  let cols = board[0].length
  let copy = new Array()
  for(let row = 0; row < rows; row++) {
    copy[row] = new Array()
    for(let col = 0; col < cols; col++) {
      copy[row][col] = board[row][col]
    }
  }

  let around = [0, -1, 1]
  for(let row = 0; row < rows; row++) {
    for(let col = 0; col < cols; col++) {
      let count = 0
      for(let i = 0; i < 3; i++) {
        for(let j = 0; j < 3; j++) {
          if(!i && !j) continue
          let r = row + around[i]
          let c = col + around[j]

          if((r >= 0 && r < rows) && (c >= 0 && c < cols) && copy[r][c] === 1){
            count++
          }
        }
      }
      if ((copy[row][col] === 1) && (count < 2 || count > 3)) {
        board[row][col] = 0;
      }
      if (copy[row][col] === 0 && count === 3) {
        board[row][col] = 1;
      }
    }
  }

};

时间复杂度:O(mn)

空间复杂度:O(mn)

思路二

我们可以把变死亡改成-1，复活改成2即可，到最后 2->1 -1->0即可

var gameOfLife = function(board) {
  if(!board.length) return
  let rows = board.length
  let cols = board[0].length

  let around = [0, -1, 1]
  for(let row = 0; row < rows; row++) {
    for(let col = 0; col < cols; col++) {
      let count = 0
      for(let i = 0; i < 3; i++) {
        for(let j = 0; j < 3; j++) {
          if(!i && !j) continue
          let r = row + around[i]
          let c = col + around[j]
          // 注意：有些位置为 -1，但是当前它还是活的，这轮过后才死
          if((r >= 0 && r < rows) && (c >= 0 && c < cols) && Math.abs(board[r][c]) === 1){
            count++
          }
        }
      }
      if ((board[row][col] === 1) && (count < 2 || count > 3)) {
        board[row][col] = -1;
      }
      if (board[row][col] === 0 && count === 3) {
        board[row][col] = 2;
      }
    }
  }
  

  for(let row = 0; row < rows; row++) {
    for(let col = 0; col < cols; col++) {
      board[row][col] = board[row][col] > 0 ? 1 : 0
    }
  }
};

时间复杂度:O(mn)

空间复杂度:O(1)

lc455. 分发饼干简单

题目描述

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

示例 2:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

思路：排序 + 贪心

升序排序，每一个试一下

var findContentChildren = function(g, s) {
    g.sort((a, b) => a - b);
    s.sort((a, b) => a - b);
    const numOfChildren = g.length, numOfCookies = s.length;
    let count = 0;
    for (let i = 0, j = 0; i < numOfChildren && j < numOfCookies; i++, j++) {
        while (j < numOfCookies && g[i] > s[j]) {
            j++;
        }
        if (j < numOfCookies) {
            count++;
        }
    }
    return count;
};

时间复杂度:O(nlogn + mlogm)

空间复杂度:O(nlogn + mlogm)

lc380. O(1) 时间插入、删除和获取随机元素简单

题目描述

实现RandomizedSet 类：

• RandomizedSet() 初始化 RandomizedSet 对象
• bool insert(int val) 当元素 val 不存在时，向集合中插入该项，并返回 true ；否则，返回 false 。
• bool remove(int val) 当元素 val 存在时，从集合中移除该项，并返回 true ；否则，返回 false 。
• int getRandom() 随机返回现有集合中的一项（测试用例保证调用此方法时集合中至少存在一个元素）。每个元素应该有 相同的概率 被返回。

你必须实现类的所有函数，并满足每个函数的 平均 时间复杂度为 O(1) 。

示例：

输入
["RandomizedSet", "insert", "remove", "insert", "getRandom", "remove", "insert", "getRandom"]
[[], [1], [2], [2], [], [1], [2], []]
输出
[null, true, false, true, 2, true, false, 2]

解释
RandomizedSet randomizedSet = new RandomizedSet();
randomizedSet.insert(1); // 向集合中插入 1 。返回 true 表示 1 被成功地插入。
randomizedSet.remove(2); // 返回 false ，表示集合中不存在 2 。
randomizedSet.insert(2); // 向集合中插入 2 。返回 true 。集合现在包含 [1,2] 。
randomizedSet.getRandom(); // getRandom 应随机返回 1 或 2 。
randomizedSet.remove(1); // 从集合中移除 1 ，返回 true 。集合现在包含 [2] 。
randomizedSet.insert(2); // 2 已在集合中，所以返回 false 。
randomizedSet.getRandom(); // 由于 2 是集合中唯一的数字，getRandom 总是返回 2 。

let RandomizedSet = function() {
    this.list = []
    this.map = {}
};

RandomizedSet.prototype.insert = function(val) {
    if(this.map[val]) return false

    this.list.push(val)
    this.map[val] = this.list.length
    return true
};

RandomizedSet.prototype.remove = function(val) {
    if(!this.map[val]) return false

    const final = this.list[this.list.length-1]

    // 下面这块主要是把要数组的尾值赋给对应的val值的位置，之后把数组最后的值踢出去即可
    const index = this.map[val]
    // 这里的index-1即我们拿到的index不是数组的下标，还需要减1。
    this.list[index-1] = final
    this.map[final] = index

    delete this.map[val]
    this.list.pop()

    return true
};

RandomizedSet.prototype.getRandom = function() {
    const index = Math.floor(Math.random() * this.list.length)
    return this.list[index]
};

lc997. 找到小镇的法官简单

题目描述

小镇里有 n 个人，按从 1 到 n 的顺序编号。传言称，这些人中有一个暗地里是小镇法官。

如果小镇法官真的存在，那么：

1. 小镇法官不会信任任何人。
2. 每个人（除了小镇法官）都信任这位小镇法官。
3. 只有一个人同时满足属性 1 和属性 2 。

给你一个数组 trust ，其中 trust[i] = [ai, bi] 表示编号为 ai 的人信任编号为 bi 的人。

如果小镇法官存在并且可以确定他的身份，请返回该法官的编号；否则，返回 -1 。

示例 1：

输入：n = 2, trust = [[1,2]]
输出：2

示例 2：

输入：n = 3, trust = [[1,3],[2,3]]
输出：3

示例 3：

输入：n = 3, trust = [[1,3],[2,3],[3,1]]
输出：-1

思路：图

法官的入度为n - 1，出度为0

var findJudge = function(n, trust) {
  // 统计每个人被信任次数和信任别人次数
  const inDegree = new Array(n + 1).fill(0);
  const outDegree = new Array(n + 1).fill(0);

  for (const [a, b] of trust) {
    outDegree[a]++;
    inDegree[b]++;
  }

  // 找法官
  for (let i = 1; i <= n; i++) {
    if (inDegree[i] === n - 1 && outDegree[i] === 0) {
      return i;
    }
  }

  return -1;
};

时间复杂度：O(T + N)，T 是 trust 数组长度，N 是人数

空间复杂度：O(N)

581. 最短无序连续子数组中等

题目描述

给你一个整数数组 nums ，你需要找出一个 连续子数组 ，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

请你找出符合题意的 最短 子数组，并输出它的长度。

示例 1：

输入：nums = [2,6,4,8,10,9,15]
输出：5
解释：你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。

示例 2：

输入：nums = [1,2,3,4]
输出：0

示例 3：

输入：nums = [1]
输出：0

排序 + 比较

var findUnsortedSubarray = function(nums) {
  if(isSort(nums)) return 0
  const sortNums = [...nums].sort((a, b) => a - b)
  let l = 0
  while(nums[l] === sortNums[l]) {
    l++
  }
  let r = nums.length - 1
  while(nums[r] === sortNums[r]) {
    r--
  }
  return r - l + 1
};

function isSort(nums) {
  for(let i = 1; i < nums.length; i++) {
    if(nums[i] < nums[i - 1]) return false
  }
  return true
}

时间复杂度:O(nlogn)

空间复杂度:O(n)

一次遍历

var findUnsortedSubarray = function(nums) {
  const n = nums.length;
  let max = -Infinity, right = -1;
  let min = +Infinity.MAX_VALUE, left = -1;
  for (let i = 0; i < n; i++) {
    if (max > nums[i]) {
      right = i;
    } else {
      max = nums[i];
    }
    if (min < nums[n - i - 1]) {
      left = n - i - 1;
    } else {
      min = nums[n - i - 1];
    }
  }
  return right === -1 ? 0 : right - left + 1;
};

时间复杂度:O(n)

空间复杂度:O(1)

lc232. 用栈实现队列简单hot

题目描述

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

• void push(int x) 将元素 x 推到队列的末尾
• int pop() 从队列的开头移除并返回元素
• int peek() 返回队列开头的元素
• boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

• 你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
• 你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例 1：

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

var MyQueue = function() {
  this.stack1 = []
  this.stack2 = []
};

/** 
 * @param {number} x
 * @return {void}
 */
MyQueue.prototype.push = function(x) {
  this.stack1.push(x)
};

/**
 * @return {number}
 */
MyQueue.prototype.pop = function() {
  if(!this.stack2.length) {
    while(this.stack1.length) {
      this.stack2.push(this.stack1.pop())
    }
  }

  return this.stack2.pop()
};

/**
 * @return {number}
 */
MyQueue.prototype.peek = function() {
  if(!this.stack2.length) {
    while(this.stack1.length) {
      this.stack2.push(this.stack1.pop())
    }
  }

  return this.stack2[this.stack2.length - 1]
};

/**
 * @return {boolean}
 */
MyQueue.prototype.empty = function() {
  return this.stack1.length === 0 && this.stack2.length === 0
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * var obj = new MyQueue()
 * obj.push(x)
 * var param_2 = obj.pop()
 * var param_3 = obj.peek()
 * var param_4 = obj.empty()
 */

lc151. 翻转字符串里的单词中等hot

题目描述

给你一个字符串 s ，逐个翻转字符串中的所有 单词 。

单词 是由非空格字符组成的字符串。s中使用至少一个空格将字符串中的 单词 分隔开。

请你返回一个翻转 s 中单词顺序并用单个空格相连的字符串。

说明：

输入字符串 s 可以在前面、后面或者单词间包含多余的空格。 翻转后单词间应当仅用一个空格分隔。 翻转后的字符串中不应包含额外的空格。

示例 1：

输入：s = "the sky is blue"
输出："blue is sky the"

示例 2：

输入：s = "  hello world  "
输出："world hello"
解释：输入字符串可以在前面或者后面包含多余的空格，但是翻转后的字符不能包括。

示例 3：

输入：s = "a good   example"
输出："example good a"
解释：如果两个单词间有多余的空格，将翻转后单词间的空格减少到只含一个。

示例 4：

输入：s = "  Bob    Loves  Alice   "
输出："Alice Loves Bob"

示例 5：

输入：s = "Alice does not even like bob"
输出："bob like even not does Alice"

法一：js api + 正则

• 去除空格

• 逆向

• 数组还原成字符串

var reverseWords = function(s) { 
  return s.trim().replace(/\s+/g, ' ').split('').reverse().join(' ')
};

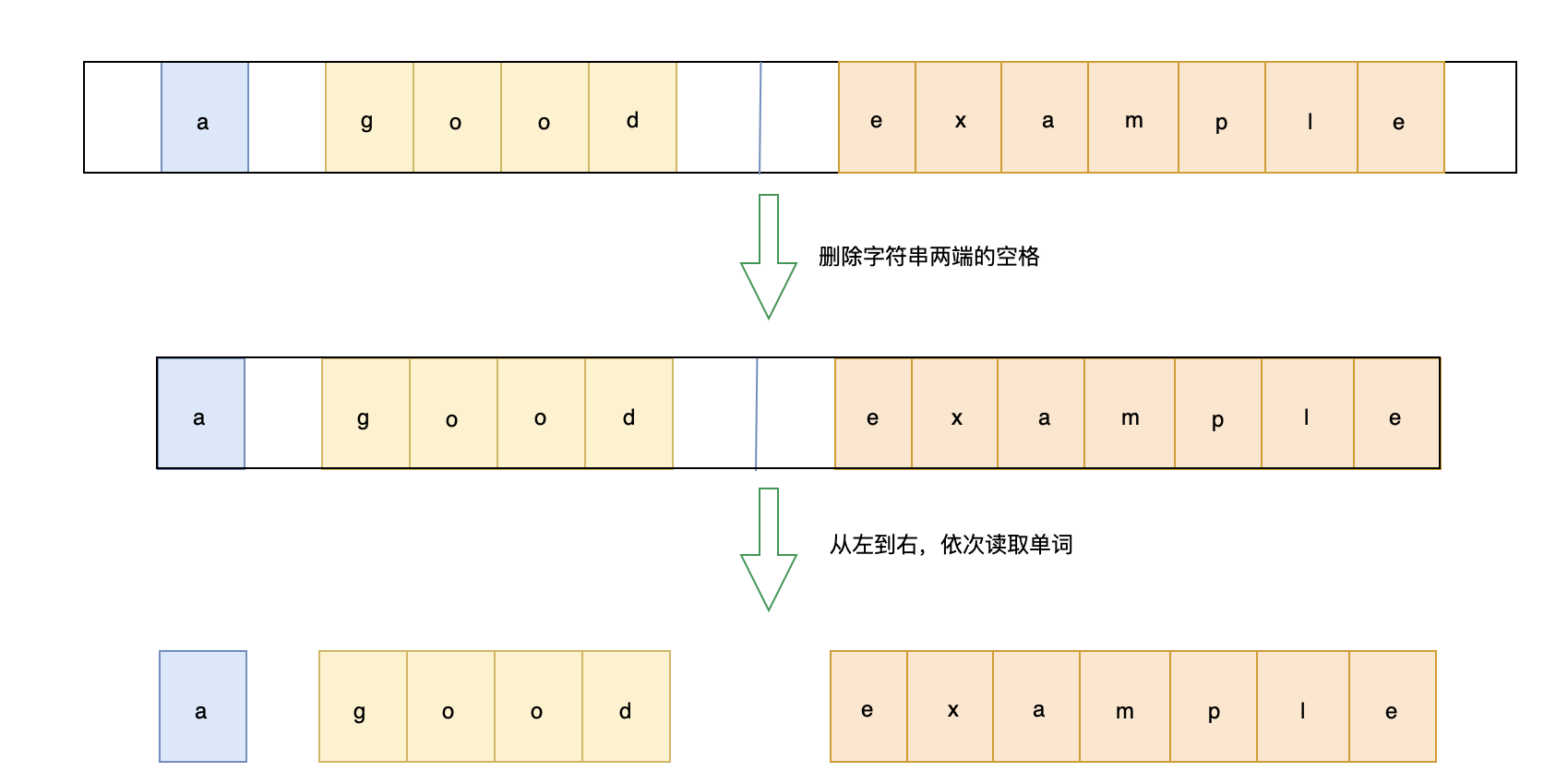
法二： 自己实现trim 和双端队列

• 首先去除字符串左右空格

• 逐个读取字符串中的每个单词，依次放入双端队列的对头

• 再将队列转换成字符串输出（已空格为分隔符）

/**
 * @param {string} s
 * @return {string}
 */
var reverseWords = function(s) {
    let left = 0
    let right = s.length - 1
    while(s.charAt(left) === ' ') left++
    while(s.charAt(right) === ' ') right--
    let word = ''
    const queue = []
    while(left <= right) {
        let char = s.charAt(left)
        if(char === ' ' && word) {
            queue.unshift(word)
            word = ''
        } else if (char !== ' ') {
            word += char
        }
        left++
    }
    queue.unshift(word)
    return queue.join(' ')
};

时间复杂度:O(n)

空间复杂度:O(n)

lc41. 缺失的第一个正数困难hot

题目描述

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

示例 1：

输入：nums = [1,2,0]
输出：3

示例 2：

输入：nums = [3,4,-1,1]
输出：2

示例 3：

输入：nums = [7,8,9,11,12]
输出：1

置换

把每个数 x 放到下标 x - 1 的位置。

步骤一：原地交换

我们遍历每个位置，如果：

• nums[i] 在合法范围（1 <= nums[i] <= n）
• 且 nums[nums[i] - 1] !== nums[i]（目标位置上的值不是正确的）

就交换 nums[i] 和 nums[nums[i] - 1]，直到它归位或者遇到重复。

步骤二：找出第一个不满足 nums[i] === i + 1 的位置

这个 i + 1 就是我们要找的最小缺失正数。

function firstMissingPositive(nums) {
  const n = nums.length;
  for (let i = 0; i < n; i++) {
    // 将 nums[i] 放到对应位置上
    while (
      // 只处理正整数，因为题目只关注最小的正整数缺失。
      nums[i] > 0 
      // 只处理范围在 [1, n] 之间的数。
			// 数组长度是 n，如果数大于 n，放到对应索引 nums[i] - 1 会越界。
      // 而且 n+1 及以上的数不影响答案，最小缺失正整数最多是 n+1。
      && nums[i] <= n 
      // 判断：目标位置上的数是不是已经是 nums[i] 了，避免无意义的交换和死循环。
      && nums[nums[i] - 1] !== nums[i]
    ) {
      const temp = nums[i];
      nums[i] = nums[temp - 1];
      nums[temp - 1] = temp;
    }
  }

  // 再次遍历，找第一个位置不对的
  for (let i = 0; i < n; i++) {
    if (nums[i] !== i + 1) {
      return i + 1;
    }
  }

  // 所有位置都对，说明是 n+1
  return n + 1;
}

时间复杂度:O(n)

空间复杂度:O(1)

470. 用 Rand7() 实现 Rand10()中等hot

题目描述

给定方法 rand7 可生成 [1,7] 范围内的均匀随机整数，试写一个方法 rand10 生成 [1,10] 范围内的均匀随机整数。

你只能调用 rand7() 且不能调用其他方法。请不要使用系统的 Math.random() 方法。

每个测试用例将有一个内部参数 n，即你实现的函数 rand10() 在测试时将被调用的次数。请注意，这不是传递给 rand10() 的参数。

示例 1:

输入: 1
输出: [2]

示例 2:

输入: 2
输出: [2,8]

示例 3:

输入: 3
输出: [3,8,10]

思路

var rand10 = function () {
  // 已知 randN() 可以等概率的生成[1, N]范围的随机数
  // 那么：(randX() - 1) × Y + randY() ==> 可以等概率的生成[1, X * Y]范围的随机数
  while (true) {
      let a = rand7()
      let b = rand7()
      // a - 1随机生成0 - 6
      // (a - 1)*7随机生成0 7 14 21 28 35 42 
      // +b后会充盈7的倍数之间的空隙
      // 所以res会是随机的[1,49]
      let res = (a - 1) * 7 + b
      // 为什么不直接在49里面模10 + 1？
      // 因为不随机了
      // 拒绝采样
      if (res <= 40) return res % 10 + 1
  }
};

时间复杂度:O(1)

空间复杂度:O(1)

860. 柠檬水找零简单

题目描述

在柠檬水摊上，每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。

每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。

注意，一开始你手头没有任何零钱。

给你一个整数数组 bills ，其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

示例 1：

输入：bills = [5,5,5,10,20]
输出：true
解释：
前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。
第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零，所以我们输出 true。

示例 2：

输入：bills = [5,5,10,10,20]
输出：false
解释：
前 2 位顾客那里，我们按顺序收取 2 张 5 美元的钞票。
对于接下来的 2 位顾客，我们收取一张 10 美元的钞票，然后返还 5 美元。
对于最后一位顾客，我们无法退回 15 美元，因为我们现在只有两张 10 美元的钞票。
由于不是每位顾客都得到了正确的找零，所以答案是 false。

var lemonadeChange = function(bills) {
  let five = 0, ten = 0
  for(let i = 0; i < bills.length; i++) {
    if(bills[i] === 5) five++
    else if(bills[i] === 10) {
      five--
      ten++
      if(five < 0) return false
    }
    else{
      if(ten > 0){
        ten--
        five--
      }else{
        five -= 3
      }
      if(five < 0) return false
      }
  }
  return true
};

时间复杂度:O(n)

空间复杂度:O(1)

55. 跳跃游戏中等

题目描述

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

解法：

我们维护一个变量 maxReach，表示当前可以跳到的最远距离。

遍历每个位置 i，如果 i 超过了 maxReach，说明你已经跳不到这个点了，直接返回 false。

否则就更新你能跳到的最远位置：maxReach = max(maxReach, i + nums[i])。

如果你一直能跳，并且 maxReach >= 最后一位，就说明可以到达。

var canJump = function(nums) {
  let maxReach = 0;
  for (let i = 0; i < nums.length; i++) {
    if (i > maxReach) return false;         // 跳不到当前位置，失败
    maxReach = Math.max(maxReach, i + nums[i]);
  }
  return true;
};

时间复杂度：O(n)，只遍历一次。

空间复杂度：O(1)，只用了一个变量。

45.跳跃游戏 II中等

题目描述

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

• 0 <= j <= nums[i]
• i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

贪心（逐步扩展「跳跃区间」）

遍历数组的过程中，维护当前能跳到的最远位置 maxReach；

每当你跳完一跳后，就更新一个新的「跳跃边界」；

记录每次到达边界就「跳一次」。

var jump = function(nums) {
  let end = 0;         // 当前跳跃的边界
  let maxReach = 0;    // 当前能跳到的最远距离
  let steps = 0;       // 跳跃次数

  for (let i = 0; i < nums.length - 1; i++) {
    maxReach = Math.max(maxReach, i + nums[i]); // 更新最远能到达的地方

    // 到达边界，必须跳一次
    if (i === end) {
      steps++;
      end = maxReach;
    }
  }

  return steps;
};

时间复杂度：O(n)，一次遍历。

空间复杂度：O(1)，只用了常数变量。

顺子数组

判断一个数组是不是“顺子”，要求：

• 数组中数字连续递增（差1），顺子长度等于数组长度
• 数组中0可以代替任何数字（即“万能牌”）

function isStraight(nums) {
  // 1. 先排序数组，方便后面检查连续和重复
  nums.sort((a, b) => a - b);

  let zeroCount = 0; // 统计0的个数
  let gap = 0;       // 非0数字之间的间隔总和

  // 2. 统计0的个数
  for (let num of nums) {
    if (num === 0) zeroCount++;
  }

  // 3. 遍历非0数字，计算间隔，判断重复
  for (let i = zeroCount + 1; i < nums.length; i++) {
    // 如果当前数字和前一个数字相同，直接返回false（不能有重复数字）
    if (nums[i] === nums[i - 1]) return false;

    // 计算两个数字之间的间隔（差值减1）
    gap += nums[i] - nums[i - 1] - 1;
  }

  // 4. 只要间隔总和 <= 0的个数，说明0足够补间隔，可以组成顺子
  return gap <= zeroCount;
}

lc994 腐烂的橘子

题目描述

• 在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

  • 值 0 代表空单元格；
  • 值 1 代表新鲜橘子；
  • 值 2 代表腐烂的橘子。

  每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

  返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

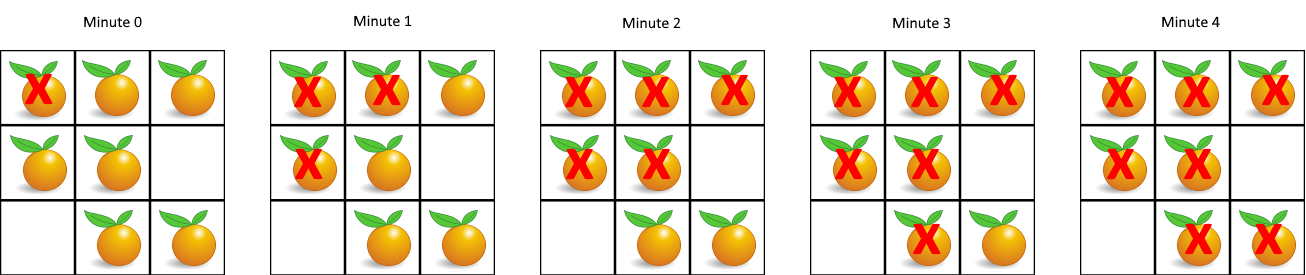
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。

示例 3：

输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

使用 多源 BFS（Breadth-First Search 广度优先搜索）：

• 将所有腐烂橘子的位置同时加入队列，作为 BFS 的起点
• 每一层 BFS 代表 1 分钟，向周围扩散腐烂状态

过程：

1. 遍历整个网格，找到所有腐烂橘子，将其坐标加入队列
2. 统计所有新鲜橘子的数量
3. 开始 BFS，队列中所有腐烂橘子同时腐烂相邻新鲜橘子，减新鲜橘子计数
4. BFS 结束后：
   • 如果还有新鲜橘子没腐烂，返回 -1
   • 否则返回经过的时间

function orangesRotting(grid) {
  const m = grid.length;
  const n = grid[0].length;
  
  let freshCount = 0;
  const queue = [];
  
  // 初始化：找到所有腐烂橘子，统计新鲜橘子数
  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (grid[i][j] === 2) {
        queue.push([i, j]);
      } else if (grid[i][j] === 1) {
        freshCount++;
      }
    }
  }
  
  if (freshCount === 0) return 0; // 没有新鲜橘子，直接返回0
  
  let minutes = 0;
  const directions = [[1,0], [-1,0], [0,1], [0,-1]];
  
  // 多源BFS开始
  while (queue.length) {
    let size = queue.length;
    let infectedThisRound = false;
    
    for (let i = 0; i < size; i++) {
      const [x, y] = queue.shift();
      
      for (const [dx, dy] of directions) {
        const nx = x + dx;
        const ny = y + dy;
        
        // 检查边界和是否为新鲜橘子
        if (nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] === 1) {
          grid[nx][ny] = 2;   // 变成腐烂橘子
          freshCount--;       // 新鲜橘子减少
          queue.push([nx, ny]);
          infectedThisRound = true;
        }
      }
    }
    
    // 只有在本轮感染了新橘子时，分钟数才增加
    if (infectedThisRound) minutes++;
  }
  
  // 如果还有新鲜橘子，说明无法腐烂
  return freshCount === 0 ? minutes : -1;
}

时间复杂度：O(m*n)，每个格子最多访问一次

空间复杂度：O(m*n)，队列最大情况是所有腐烂橘子

lc763. 划分字母区间

题目描述

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。例如，字符串 "ababcc" 能够被分为 ["abab", "cc"]，但类似 ["aba", "bcc"] 或 ["ab", "ab", "cc"] 的划分是非法的。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表。

示例 1：

输入：s = "ababcbacadefegdehijhklij"
输出：[9,7,8]
解释：
划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的，因为划分的片段数较少。 

示例 2：

输入：s = "eccbbbbdec"
输出：[10]

思路: 贪心

1. 统计每个字母最后一次出现的位置
2. 遍历字符串，维护一个变量 end 表示当前分割的最大结束位置，更新为遍历过的字符最后一次出现位置的最大值。
3. 当遍历索引达到 end，说明当前片段可以结束，把长度加入结果，更新下一个片段的起点。

var partitionLabels = function(s) {
  const last = new Map();
  // 记录每个字符的最后出现位置
  for (let i = 0; i < s.length; i++) {
    last.set(s[i], i);
  }

  const result = [];
  let start = 0, end = 0;

  for (let i = 0; i < s.length; i++) {
    // 更新当前片段的结束位置
    end = Math.max(end, last.get(s[i]));

    // 到达片段末尾
    if (i === end) {
      result.push(end - start + 1);
      start = i + 1;
    }
  }

  return result;
};