 动态规划
动态规划
# 动态规划
# lc91. 解码方法中等
题目描述
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
'A' -> 1
'B' -> 2
...
'Z' -> 26
2
3
4
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,"11106" 可以映射为:
"AAJF",将消息分组为(1 1 10 6)"KJF",将消息分组为(11 10 6)
注意,消息不能分组为 (1 11 06) ,因为 "06" 不能映射为 "F" ,这是由于 "6" 和 "06" 在映射中并不等价。
给你一个只含数字的 非空 字符串 s ,请计算并返回 解码 方法的 总数 。
题目数据保证答案肯定是一个 32 位 的整数。
示例 1:
输入:s = "12"
输出:2
解释:它可以解码为 "AB"(1 2)或者 "L"(12)。
2
3
示例 2:
输入:s = "226"
输出:3
解释:它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。
2
3
示例 3:
输入:s = "0"
输出:0
解释:没有字符映射到以 0 开头的数字。
含有 0 的有效映射是 'J' -> "10" 和 'T'-> "20" 。
由于没有字符,因此没有有效的方法对此进行解码,因为所有数字都需要映射。
2
3
4
5
示例 4:
输入:s = "06"
输出:0
解释:"06" 不能映射到 "F" ,因为字符串含有前导 0("6" 和 "06" 在映射中并不等价)。
2
3
思路:动态规划
对于字符串 s 的任意位置 i 而言,其存在三种情况:
只能由位置
i的单独作为一个item,设为a,转移的前提是a的数值范围为[1,9],转移逻辑为f[i] = f[i - 1]。只能由位置
i的与前一位置(i-1)共同作为一个item,设为b,转移的前提是b的数值范围为[10,26],转移逻辑为f[i] = f[i - 2]。位置
i既能作为独立item也能与上一位置形成item,转移逻辑为f[i] = f[i - 1] + f[i - 2]。因此,我们有如下转移方程:
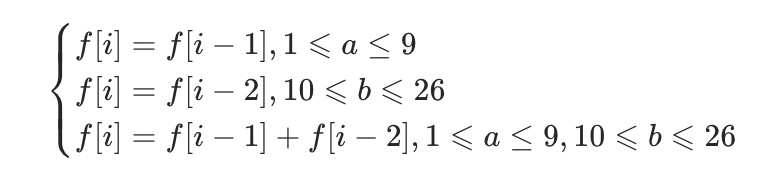
其他细节:由于题目存在前导零,而前导零属于无效 item。可以进行特判,但个人习惯往字符串头部追加空格作为哨兵,追加空格既可以避免讨论前导零,也能使下标从 1 开始,简化 f[i-1] 等负数下标的判断。
var numDecodings = function(s) {
const len = s.length
const dp = new Array(len + 1).fill(0)
dp[0] = 1
s = ' ' + s
for(let i = 1; i <= len; i++) {
// a : 代表「当前位置」单独形成 item
// b : 代表「当前位置」与「前一位置」共同形成 item
let a = s[i] - '0', b = (s[i - 1] - '0') * 10 + (s[i] - '0');
// 如果 a 属于有效值,那么 dp[i] 可以由 dp[i - 1] 转移过来
if (1 <= a && a <= 9) dp[i] = dp[i - 1];
// 如果 b 属于有效值,那么 dp[i] 可以由 dp[i - 2] 或者 dp[i - 1] & dp[i - 2] 转移过来
if (10 <= b && b <= 26) dp[i] += dp[i - 2];
}
return dp[len]
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
时间复杂度:O(n)
空间复杂度:O(n)
简化: f[i] 时只依赖 f[i-1] 和 f[i-2] 两个状态
var numDecodings = function(s) {
const len = s.length
const dp = new Array(3).fill(0)
dp[0] = 1
s = ' ' + s
for(let i = 1; i <= len; i++) {
dp[i % 3] = 0
let a = s[i] - '0', b = (s[i - 1] - '0') * 10 + (s[i] - '0');
// 如果 a 属于有效值,那么 dp[i] 可以由 dp[i - 1] 转移过来
if (1 <= a && a <= 9) dp[i % 3] = dp[(i - 1) % 3];
// 如果 b 属于有效值,那么 dp[i] 可以由 dp[i - 2] 或者 dp[i - 1] & dp[i - 2] 转移过来
if (10 <= b && b <= 26) dp[i % 3] += dp[(i - 2) % 3];
}
return dp[len % 3]
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
时间复杂度:O(n)
空间复杂度:O(1)
# lc05. 最长回文子串中等hot
题目描述
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
2
3
示例 2:
输入:s = "cbbd"
输出:"bb"
2
示例 3:
输入:s = "a"
输出:"a"
2
示例 4:
输入:s = "ac"
输出:"a"
2
思路
就是以字符串的每一个字符为中心点,然后分别向左和向右进行延伸
var longestPalindrome = function(s) {
if (s.length < 2) return s;
let start = 0, end = 0;
const expandAroundCenter = (left, right) => {
while (left >= 0 && right < s.length && s[left] === s[right]) {
left--;
right++;
}
return [left + 1, right - 1];
};
for (let i = 0; i < s.length; i++) {
let [left1, right1] = expandAroundCenter(i, i); // 奇数中心
let [left2, right2] = expandAroundCenter(i, i + 1); // 偶数中心
if (right1 - left1 > end - start) {
start = left1;
end = right1;
}
if (right2 - left2 > end - start) {
start = left2;
end = right2;
}
}
return s.slice(start, end + 1);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
时间复杂度:O(n^2)
空间复杂度O(1)
# lc279. 完全平方数中等
题目描述
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
2
3
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
2
3
思路
定义 dp[i] 表示组成数字 i 所需的最少完全平方数个数。
初始时,dp[0] = 0。
对每个 i 从 1 到 n,枚举所有小于等于 i 的完全平方数 j*j,尝试更新 dp[i]:
dp[i]=min(dp[i],dp[i−j∗j]+1)
var numSquares = function(n) {
const dp = new Array(n + 1).fill(Infinity);
dp[0] = 0;
for (let i = 1; i <= n; i++) {
for (let j = 1; j * j <= i; j++) {
dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
}
}
return dp[n];
};
2
3
4
5
6
7
8
9
10
11
12
时间复杂度:O(n sqrtn)
空间复杂度:O(n)
